
【题目】绘制函数![]() 的图象,我们经历了如下过程:确定自变量
的图象,我们经历了如下过程:确定自变量![]() 的取值范围是
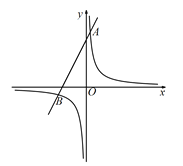
的取值范围是![]() ;列表-描点--连线,得到该函数的图象如图所示
;列表-描点--连线,得到该函数的图象如图所示
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
观察函数图象,回答下列问题:
(1)函数图象在第 象限;
(2)函数图象的对称性是
B.只是轴对称图形,不是中心对称图形
A.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
C.不是轴对称图形,而是中心对称图形
(3)在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
(4)方程![]() 是否有实数解?说明
是否有实数解?说明
【答案】. (1)函数图象在第一、三象限;(2)![]() ;(3)
;(3)![]() ,小,
,小,![]() ; x=-1,大,
; x=-1,大,![]() ;(4)方程
;(4)方程![]() 没有实数解.
没有实数解.
【解析】
根据题中题干的表格,在平面直角坐标系中描出相应的点,然后用平滑的曲线作出函数图象,如图所示:
(1)由函数图象可知:函数图象位于第一、三象限;
(2)由函数图象可知:该函数图象为中心对称图形,不是轴对称图形;
(3)当x大于0时,函数图象为第一象限部分,有最低点,可得当x=1时,y有最小值为2;当x小于0时,函数图象为第三象限部分,有最高点,可得当x=-1时,y有最大值-2;
(4)所求方程没有实数根,理由为:所求方程可看做函数y=x+![]() 与y=-2x+1的交点横坐标,由图形可知两函数图象没有交点,故所求方程没有实数根.
与y=-2x+1的交点横坐标,由图形可知两函数图象没有交点,故所求方程没有实数根.
解:作出函数图象,如图所示:
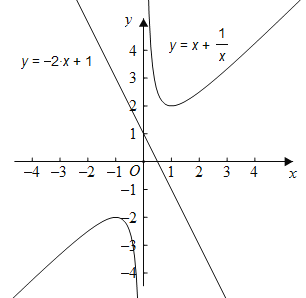
(1)函数图象在第一、三象限;
(2)函数图象不是轴对称图形,而是中心对称图形,选C;
(3)在x>0时,当x=1时,函数y有最小值,且这个最值等于2;
在x<0时,当x=-1时,函数y有最大值,且这个最值等于-2;
(4)方程x+![]() =-2x+1没有实数解,理由为:y=x+
=-2x+1没有实数解,理由为:y=x+![]() 与y=-2x+1在同一直角坐标系中无交点.
与y=-2x+1在同一直角坐标系中无交点.
故答案为:(1)一、三;(2)C;(3)1,小,2;-1,大,-2


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】我市实施城乡生活垃圾分类管理,推进生态文明建设为增强学生的环保意识,随机抽取![]() 名学生,对他们的垃圾分类投放情况进行调查,这
名学生,对他们的垃圾分类投放情况进行调查,这![]() 名学生分别标记为
名学生分别标记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求![]() 名学生中至少有三类垃圾投放正确的概率;
名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从![]() 名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果,并求出刚好抽到
名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果,并求出刚好抽到![]() 、
、![]() 两位学生的概率.
两位学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠病毒潜伏期较长,能通过多种渠道传播,以在生活中就要做好最基本的防护:在公共区域和陌生人保持距离,勤洗手,出门戴口罩某区中小学陆续复学后,为了提高同学们的防疫意识,决定组织防疫知识竞赛活动,评出一、二三等奖各若干名,并分别发给洗手液、温度计和口罩作为奖品.
(1)如果温度计的单价比口罩的单价多![]() 元,购买洗手液
元,购买洗手液![]() 瓶和口罩
瓶和口罩![]() 个共需
个共需![]() 元;购买
元;购买![]() 瓶洗手液比购买
瓶洗手液比购买![]() 支温度计多花
支温度计多花![]() 元,求洗手液、温度计和口罩的单价各是多少元?
元,求洗手液、温度计和口罩的单价各是多少元?
(2)已知本次竞赛活动获得三等奖的人数是获得二等奖人数的![]() 倍,且获得一等奖的人数不超过获奖总人数的五分之一,如果购买这三种奖品的总费用为
倍,且获得一等奖的人数不超过获奖总人数的五分之一,如果购买这三种奖品的总费用为![]() 元,求本次竞赛活动获得一、二、三等奖各有多少人.
元,求本次竞赛活动获得一、二、三等奖各有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乒乓球是我国的国球,比赛采用单局![]() 分制,分团体、单打、双打等。在某站公开赛中,某直播平台同时直播
分制,分团体、单打、双打等。在某站公开赛中,某直播平台同时直播![]() 场男单四分之一决赛,四场比赛的球桌号分别为“
场男单四分之一决赛,四场比赛的球桌号分别为“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”(假设
”(假设![]() 场比赛同时开始),小宁和父亲准备一同观看其中的一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“
场比赛同时开始),小宁和父亲准备一同观看其中的一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”的四张卡片(除数字不同外,其余均相同)分别对应球桌号“
”的四张卡片(除数字不同外,其余均相同)分别对应球桌号“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”,卡片洗匀后背面朝上放在桌子上,父亲先从中随机抽取一张,小宁再从剩下的
”,卡片洗匀后背面朝上放在桌子上,父亲先从中随机抽取一张,小宁再从剩下的![]() 张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛。
张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛。
(1)下列事件中属于必然事件的是 .
A.抽到的是小宁最终想要看的一场比赛的球桌号
B.抽到的是父亲最终想要看的一场比赛的球桌号
C.小宁和父亲抽到同一个球桌号
D.小宁和父亲抽到的球桌号不一样
(2)用列表法或树状图法求小宁和父亲最终观看“T”球桌比赛的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
(1)①M{(﹣2)2,22,﹣22}= ; ②min{sin30°,cos60°,tan45°}= ;
(2)若M{﹣2x,x2,3}=2,求x的值;
(3)若min{3﹣2x,1+3x,﹣5}=﹣5,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 点
点![]() 是
是![]() 边上一点,
边上一点,![]() 点
点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰
的下方作等腰![]() 连接
连接![]() 当
当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止的过程中,
停止的过程中,![]() 面积的最大值等于_____________________
面积的最大值等于_____________________![]()
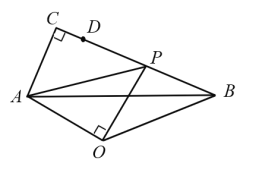
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=6,将Rt△ABC绕点C顺时针旋转,使斜边A′B′过B点,则线段CA扫过的面积为_____.(结果保留根号和π)
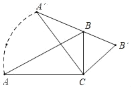
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面系中,一次函数![]() 的图像经过定点A,反比例函数
的图像经过定点A,反比例函数![]() 的图像经过点A,且与一次函数
的图像经过点A,且与一次函数![]() 的图像相交于点B(
的图像相交于点B(![]() ,m).
,m).
(1)求m、a的值;
(2)设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com