
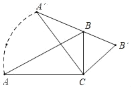
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=6,将Rt△ABC绕点C顺时针旋转,使斜边A′B′过B点,则线段CA扫过的面积为_____.(结果保留根号和π)
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
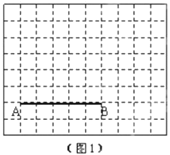
【题目】图1、图2分别是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段![]() 的两个端点均在小正方形的顶点上.
的两个端点均在小正方形的顶点上.
(1)在图1中画出以![]() 为直角边的直角
为直角边的直角![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() ;
;
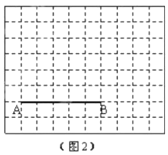
(2)在图2中画出以![]() 为腰的钝角等腰
为腰的钝角等腰![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() 的面积为10.并直接写出线段
的面积为10.并直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B分别在反比例函数![]() (x>0),
(x>0),![]() (k<0,x>0)的图象上.点B的横坐标为4,且点B在直线y=x﹣5上.
(k<0,x>0)的图象上.点B的横坐标为4,且点B在直线y=x﹣5上.
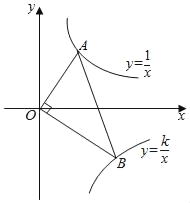
(1)求k的值;(2)若OA⊥OB,求tan∠ABO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
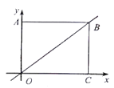
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 分别在坐标轴的正半轴上,
分别在坐标轴的正半轴上, ![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与折线
与折线![]() 有公共点.
有公共点.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)对于一次函数![]() ,当
,当![]() 随
随![]() 的增大而减小时,直接写出
的增大而减小时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
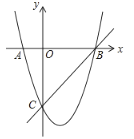
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求抛物线的解析式;
(2)过点![]() 作直线
作直线![]() 轴交抛物线于另一点
轴交抛物线于另一点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在二次函数的学习中,教材有如下内容:
例1 函数图象求一元二次方程![]() 的近似解(精确到0.1).
的近似解(精确到0.1).
解:设有二次函数![]() ,列表并作出它的图象(图1).
,列表并作出它的图象(图1).
| … |
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
| … |
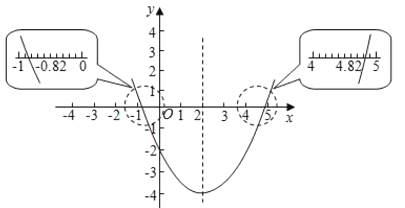
观察抛物线和![]() 轴交点的位置,估计出交点的横坐标分别约为
轴交点的位置,估计出交点的横坐标分别约为![]() 和4.8,所以得出方程精确到0.1的近似解为
和4.8,所以得出方程精确到0.1的近似解为![]() ,
,![]() ,利用二次函数
,利用二次函数![]() 的图象求出一元二次方程
的图象求出一元二次方程![]() 的解的方法称为图象法,这种方法常用来求方程的近似解.
的解的方法称为图象法,这种方法常用来求方程的近似解.
小聪和小明通过例题的学习,体会到利用函数图象可以求出方程的近似解.于是他们尝试利用图象法探宄方程![]() 的近似解,做法如下:
的近似解,做法如下:
小聪的做法:令函数![]() ,列表并画出函数的图象,借助图象得到方程
,列表并画出函数的图象,借助图象得到方程![]() 的近似解.
的近似解.
小明的做法:因为![]() ,所以先将方程
,所以先将方程![]() 的两边同时除以
的两边同时除以![]() ,变形得到方程
,变形得到方程![]() ,再令函数
,再令函数![]() 和
和![]() ,列表并画出这两个函数的图象,借助图象得到方程
,列表并画出这两个函数的图象,借助图象得到方程![]() 的近似解.
的近似解.
请你选择小聪或小明的做法,求出方程![]() 的近似解(精确到0.1).
的近似解(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com