
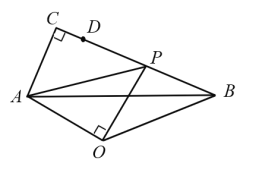
【题目】如图,![]() 中,
中,![]() 点
点![]() 是
是![]() 边上一点,
边上一点,![]() 点
点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰
的下方作等腰![]() 连接
连接![]() 当
当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止的过程中,
停止的过程中,![]() 面积的最大值等于_____________________
面积的最大值等于_____________________![]()
【答案】![]()
【解析】
设![]() ①当
①当![]() 时,作
时,作![]() 于
于![]() 于
于![]() .先证明
.先证明![]() ,进而可得四边形
,进而可得四边形![]() 是正方形;设
是正方形;设![]() ,用x、y表示出PB和OH,然后运用三角形的面积公式二次函数求最值即可;②当
,用x、y表示出PB和OH,然后运用三角形的面积公式二次函数求最值即可;②当![]() 时,同理(1)可得
时,同理(1)可得![]() ,根据二次函数的性质可得,当x=4时有最大值.然后比较即可确定最大值.
,根据二次函数的性质可得,当x=4时有最大值.然后比较即可确定最大值.
解:设![]()
①如图1,当![]() 时,作
时,作![]() 于
于![]() 于
于![]() .
.
∴∠OHP=∠OGA=90°
∵四边形AOPC中,∠C=90°,∠AOP=90°
∴∠CAB+∠OPC=180°
∵∠BPO+∠OPC=180°
∴∠OPH=∠OAG
∵在△AOG和△POH
∠OHP=∠OGA,∠OPH=∠OAG,AO=OP
∴![]() ,
,
∴OH=OG
∵∠OHP=∠OGA=∠C=90°
∴四边形![]() 是正方形
是正方形
设![]() ,则
,则![]() ,得
,得![]() ,即有
,即有![]() .
.
∴![]()
∴![]()
所以当![]() 时,
时,![]()

②如图2,当![]() 时,同理可得
时,同理可得![]()
所以当x=4时,![]()
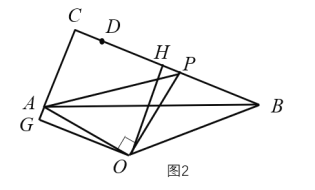
综上,当![]() 时,
时,![]() .
.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图①,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,将直线
的中点,将直线![]() 向右平移
向右平移![]() 个单位长度,
个单位长度,![]() 、
、![]() 、
、![]() 的对应点为
的对应点为![]() 、
、![]() 、
、![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,连接
,连接![]() 、
、![]() .
.
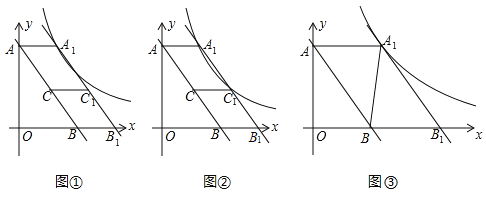
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)如图②, 当反比例函数的图象经过点![]() 时, 求四边形
时, 求四边形![]() 的面积;
的面积;
(3)如图③,连接![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,已知锐角![]() 内有定点
内有定点![]() ,过点
,过点![]() 任意作一条直线
任意作一条直线![]() ,分别交射线
,分别交射线![]() ,
,![]() 于点M,N.若
于点M,N.若![]() 是线段
是线段![]() 的中点时,则称直线
的中点时,则称直线![]() 是
是![]() 的中点直线.如图2,射线
的中点直线.如图2,射线![]() 的解析式为
的解析式为![]() 与
与![]() 轴的夹角为
轴的夹角为![]() ,
,![]() ,
,![]() 为
为![]() 的中点直线.
的中点直线.
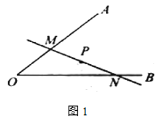
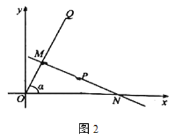
(1)求直线![]() 的解析式;
的解析式;
(2)若过点![]() 任意作一条直线
任意作一条直线![]() ,分别交射线
,分别交射线![]() ,
,![]() 轴的正半轴于点
轴的正半轴于点![]() ,
,![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绘制函数![]() 的图象,我们经历了如下过程:确定自变量
的图象,我们经历了如下过程:确定自变量![]() 的取值范围是
的取值范围是![]() ;列表-描点--连线,得到该函数的图象如图所示
;列表-描点--连线,得到该函数的图象如图所示
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
观察函数图象,回答下列问题:
(1)函数图象在第 象限;
(2)函数图象的对称性是
B.只是轴对称图形,不是中心对称图形
A.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
C.不是轴对称图形,而是中心对称图形
(3)在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
(4)方程![]() 是否有实数解?说明
是否有实数解?说明
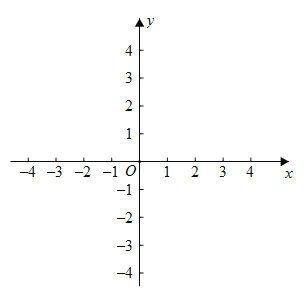
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上不同于
上不同于![]() 的两点,连接
的两点,连接![]() 且
且![]() 过点
过点![]() 作
作![]() 垂足为
垂足为![]() 直线
直线![]() 与
与![]() 相交于点
相交于点![]() .
.
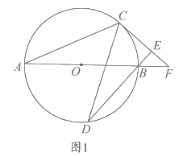
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]()
①求直径![]() 的长;
的长;
②如图2所示,连接![]() 直接写出
直接写出![]() 的面积与四边形
的面积与四边形![]() 的面积的比值 .
的面积的比值 .
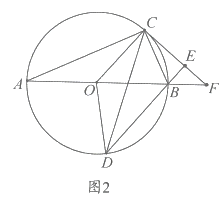
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车行去年A型车的销售总额为6万元,今年每辆车的售价比去年减少400元.若卖出的数量相同,销售总额将比去年减少20%.
(1)求今年A型车每辆车的售价.
(2)该车行计划新进一批A型车和B型车共45辆,已知A、B型车的进货价格分别是1100元,1400元,今年B型车的销售价格是2000元,要求B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京和上海都有检测新冠肺炎病毒的仪器可供外地使用,其中北京有![]() 台,上海有
台,上海有![]() 台.
台.
(1)已知武汉需要![]() 台,温州需要
台,温州需要![]() 台,从北京、上海将仪器运往武汉、温州的费用如下表所示,有关部门计划用
台,从北京、上海将仪器运往武汉、温州的费用如下表所示,有关部门计划用![]() 元运送这些仪器.请你设计一种运送方案,使武汉、温州能得到所需仪器,而且运费正好够用.
元运送这些仪器.请你设计一种运送方案,使武汉、温州能得到所需仪器,而且运费正好够用.
(2)为了节约运送资金,中央防控工作组统一调配仪器,分配到温州的仪器不能超过![]() 台,则如何调配?
台,则如何调配?
终点 起点 | 温州 | 武汉 |
北京 |
|
|
上海 |
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com