
【题目】如图,已知![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 关于
关于![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 上.
上.
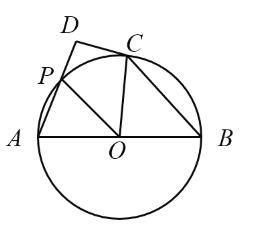
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 的切线
的切线![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .如果
.如果![]() ,求
,求![]() 的直径.
的直径.
【答案】(1)见解析;(2)4
【解析】
(1)由题意可知![]() ,根据同弧所对的圆心角相等得到
,根据同弧所对的圆心角相等得到![]() ,再根据同弧所对的圆心角和圆周角的关系得出
,再根据同弧所对的圆心角和圆周角的关系得出![]() ,利用同位角相等两直线平行,可得出PO与BC平行;
,利用同位角相等两直线平行,可得出PO与BC平行;
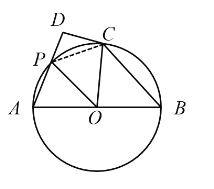
(2)利用切线的性质得到OC垂直于CD,从而得到OC∥AD,即可得到∠APO=∠COP,进一步得出∠APO=∠AOP,确定出![]() 为等边三角形,点
为等边三角形,点![]() ,点
,点![]() 关于
关于![]() 对称,继而得出
对称,继而得出![]() 为等边三角形,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,可得出PD为AB的四分之一,即AB=4PD=4.
为等边三角形,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,可得出PD为AB的四分之一,即AB=4PD=4.
解:(1)证明:∵点![]() 关于
关于![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 上.
上.
∴![]() ∴
∴![]() ,∴
,∴![]()
又∵![]() ∴
∴![]() ,
,
∴![]() ;
;
(2)解:连接![]() ,
,
∵![]() 为圆
为圆![]() 的切线,∴
的切线,∴![]() ,又
,又![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ∵
∵![]() .
.
∴![]() 为等边三角形,
为等边三角形,![]() ,
,
又∵点![]() ,点
,点![]() 关于
关于![]() 对称
对称
∴![]() 也为等边三角形,
也为等边三角形,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
在![]() 中
中![]() ,
,
又![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
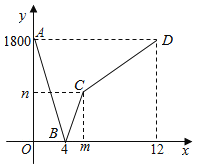
【题目】甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为![]() (小时),两车之间的阻离为
(小时),两车之间的阻离为![]() (千米),图中的折线表示
(千米),图中的折线表示![]() 与
与![]() 之间的函数关系,则图中
之间的函数关系,则图中![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
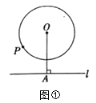
【题目】问题探究
(1)如图①,已知![]() 与直线
与直线![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,则圆上一点
,则圆上一点![]() 到
到![]() 的距离的最小值是______;
的距离的最小值是______;
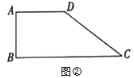
(2)如图②,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作一条直线交边
作一条直线交边![]() 或
或![]() 于
于![]() ,若
,若![]() 平分四边形
平分四边形![]() 的面积,求
的面积,求![]() 的长;
的长;
问题解决
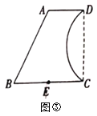
(3)如图③所示,是由线段![]() 、
、![]() 、
、![]() 与弧
与弧![]() 围成的花园的平面示意图,
围成的花园的平面示意图,![]() ,
,![]() ,
,![]() //
//![]() ,CD⊥BC,点
,CD⊥BC,点![]() 为
为![]() 的中点,
的中点,![]() 所对的圆心角为
所对的圆心角为![]() .管理人员想在
.管理人员想在![]() 上确定一点
上确定一点![]() ,在四边形
,在四边形![]() 区域种植花卉,其余区域种植草坪,并过
区域种植花卉,其余区域种植草坪,并过![]() 点修建一条小路
点修建一条小路![]() ,把四边形
,把四边形![]() 分成面积相等且尽可能小的两部分,分别种植不同的花卉.问是否存在满足上述条件的小路
分成面积相等且尽可能小的两部分,分别种植不同的花卉.问是否存在满足上述条件的小路![]() ?若存在,请求出
?若存在,请求出![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乒乓球是我国的国球,比赛采用单局![]() 分制,分团体、单打、双打等。在某站公开赛中,某直播平台同时直播
分制,分团体、单打、双打等。在某站公开赛中,某直播平台同时直播![]() 场男单四分之一决赛,四场比赛的球桌号分别为“
场男单四分之一决赛,四场比赛的球桌号分别为“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”(假设
”(假设![]() 场比赛同时开始),小宁和父亲准备一同观看其中的一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“
场比赛同时开始),小宁和父亲准备一同观看其中的一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”的四张卡片(除数字不同外,其余均相同)分别对应球桌号“
”的四张卡片(除数字不同外,其余均相同)分别对应球桌号“![]() ”,“
”,“![]() ”,“
”,“![]() ”,“
”,“![]() ”,卡片洗匀后背面朝上放在桌子上,父亲先从中随机抽取一张,小宁再从剩下的
”,卡片洗匀后背面朝上放在桌子上,父亲先从中随机抽取一张,小宁再从剩下的![]() 张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛。
张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛。
(1)下列事件中属于必然事件的是 .
A.抽到的是小宁最终想要看的一场比赛的球桌号
B.抽到的是父亲最终想要看的一场比赛的球桌号
C.小宁和父亲抽到同一个球桌号
D.小宁和父亲抽到的球桌号不一样
(2)用列表法或树状图法求小宁和父亲最终观看“T”球桌比赛的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
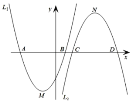
【题目】如图,已知二次函数![]() :
:![]() 和二次函数
和二次函数![]() :
:![]()
![]() 图象的顶点分别为
图象的顶点分别为![]() 、
、![]() ,与
,与![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)和
的左边)和![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),
的左边),
(1)函数![]() 的顶点坐标为______;当二次函数
的顶点坐标为______;当二次函数![]() ,
,![]() 的
的![]() 值同时随着
值同时随着![]() 的增大而增大时,则
的增大而增大时,则![]() 的取值范围是_______;
的取值范围是_______;
(2)判断四边形![]() 的形状(直接写出,不必证明);
的形状(直接写出,不必证明);
(3)抛物线![]() ,
,![]() 均会分别经过某些定点;
均会分别经过某些定点;
①求所有定点的坐标;
②若抛物线![]() 位置固定不变,通过平移抛物线
位置固定不变,通过平移抛物线![]() 的位置使这些定点组成的图形为菱形,则抛物线
的位置使这些定点组成的图形为菱形,则抛物线![]() 应平移的距离是多少?
应平移的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
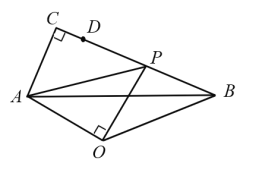
【题目】如图,![]() 中,
中,![]() 点
点![]() 是
是![]() 边上一点,
边上一点,![]() 点
点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰
的下方作等腰![]() 连接
连接![]() 当
当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止的过程中,
停止的过程中,![]() 面积的最大值等于_____________________
面积的最大值等于_____________________![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
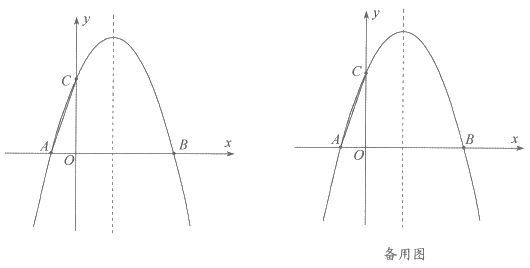
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,点
两点,点![]() 坐标为
坐标为![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]()
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴右侧抛物线图像上的一动点,设点
轴右侧抛物线图像上的一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①是否存在这样的点![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
②若该动点![]() 在第一象限内,连接
在第一象限内,连接![]() ,当
,当![]() 时,求
时,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
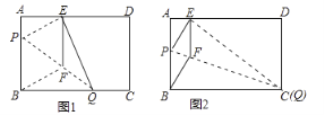
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,拆痕为
处,拆痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() 、
、![]() 也随之移动;
也随之移动;
①当点![]() 与点
与点![]() 重合时(如图2),求菱形
重合时(如图2),求菱形![]() 的边长;
的边长;
②若限定![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上移动,求
上移动,求![]() 的内切圆半径的取值范围.
的内切圆半径的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学八年级一班开展了“读一本好书”的活动,委会对学生阅读书籍的情况行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布直方图和扇形统计图.根据图表提供的信息,回答下列问题:
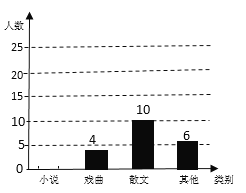
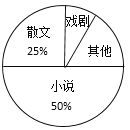
(1)八年级一班有多少名学生?
(2)请补全频数分布直方图,在扇形统计图中,“戏剧”类对应的扇形圆心角是多少度?
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出![]() 名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的
名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的![]() 人恰好是甲和丙的概率.
人恰好是甲和丙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com