
【题目】如图1,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上不同于
上不同于![]() 的两点,连接
的两点,连接![]() 且
且![]() 过点
过点![]() 作
作![]() 垂足为
垂足为![]() 直线
直线![]() 与
与![]() 相交于点
相交于点![]() .
.
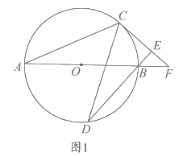
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]()
①求直径![]() 的长;
的长;
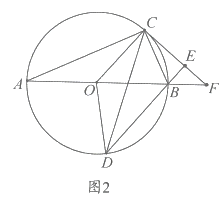
②如图2所示,连接![]() 直接写出
直接写出![]() 的面积与四边形
的面积与四边形![]() 的面积的比值 .
的面积的比值 .
【答案】(1)证明见解析;(2)①![]() ;②
;②![]()
【解析】
(1) 连接![]() ,根据圆周角定理得到
,根据圆周角定理得到![]() ,因此得到
,因此得到![]() ,再根据
,再根据![]() 以及直线平行的性质即可证明;
以及直线平行的性质即可证明;
(2) ①由![]() 得
得![]() ,假设
,假设![]() ,根据
,根据![]() 即可计算r的值,进而得到直径AB的值;
即可计算r的值,进而得到直径AB的值;
②作![]() 于
于![]() 先根据垂径定理算出BD=9,再设
先根据垂径定理算出BD=9,再设![]() 中
中![]() 边的高长度为
边的高长度为![]() ,设
,设![]() 中
中![]() 边的高长度为
边的高长度为![]() ,根据
,根据![]() 即可算出答案;
即可算出答案;
解:(1)连接![]() ,
,
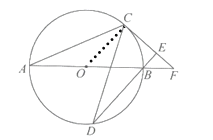
∵![]() (圆周角定理),
(圆周角定理),
∴![]()
∴![]() (内错角相等,两直线平行),
(内错角相等,两直线平行),
又由![]()
∴![]()
∴![]() (两直线平行,同旁内角互补),
(两直线平行,同旁内角互补),
故![]() 与
与![]() 相切.
相切.
(2)①如图,
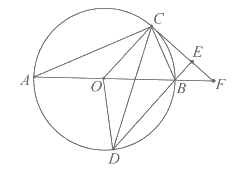
由(1)知![]() (两直线平行,同位角相等),
(两直线平行,同位角相等),
又![]() (同弧圆周角相等),
(同弧圆周角相等),
∴![]()
∴![]() ,
,
设![]() ,
,
则![]() ,
,
于是![]()
解得![]() ,
,
则![]() .
.
②如图1,作![]() 于
于![]()
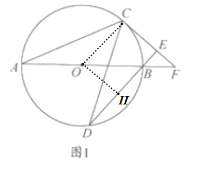
则![]()
由垂径定理得![]() .
.
如图2,设![]() 中
中![]() 边的高长度为
边的高长度为![]() ,设
,设![]() 中
中![]() 边的高长度为
边的高长度为![]() ,
,
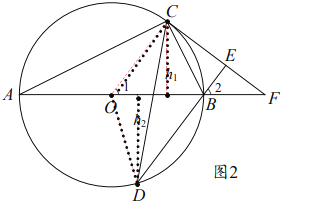
则![]()
记![]() ,
,
则![]() ,
,![]() ,
,
得面积比为![]() ;
;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】新冠病毒潜伏期较长,能通过多种渠道传播,以在生活中就要做好最基本的防护:在公共区域和陌生人保持距离,勤洗手,出门戴口罩某区中小学陆续复学后,为了提高同学们的防疫意识,决定组织防疫知识竞赛活动,评出一、二三等奖各若干名,并分别发给洗手液、温度计和口罩作为奖品.
(1)如果温度计的单价比口罩的单价多![]() 元,购买洗手液
元,购买洗手液![]() 瓶和口罩
瓶和口罩![]() 个共需
个共需![]() 元;购买
元;购买![]() 瓶洗手液比购买
瓶洗手液比购买![]() 支温度计多花
支温度计多花![]() 元,求洗手液、温度计和口罩的单价各是多少元?
元,求洗手液、温度计和口罩的单价各是多少元?
(2)已知本次竞赛活动获得三等奖的人数是获得二等奖人数的![]() 倍,且获得一等奖的人数不超过获奖总人数的五分之一,如果购买这三种奖品的总费用为
倍,且获得一等奖的人数不超过获奖总人数的五分之一,如果购买这三种奖品的总费用为![]() 元,求本次竞赛活动获得一、二、三等奖各有多少人.
元,求本次竞赛活动获得一、二、三等奖各有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
(1)①M{(﹣2)2,22,﹣22}= ; ②min{sin30°,cos60°,tan45°}= ;
(2)若M{﹣2x,x2,3}=2,求x的值;
(3)若min{3﹣2x,1+3x,﹣5}=﹣5,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 点
点![]() 是
是![]() 边上一点,
边上一点,![]() 点
点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰
的下方作等腰![]() 连接
连接![]() 当
当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止的过程中,
停止的过程中,![]() 面积的最大值等于_____________________
面积的最大值等于_____________________![]()
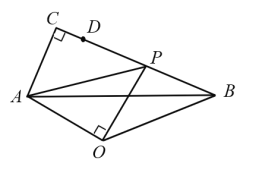
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
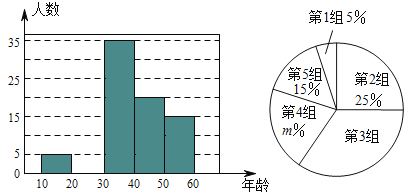
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
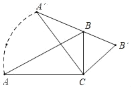
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=6,将Rt△ABC绕点C顺时针旋转,使斜边A′B′过B点,则线段CA扫过的面积为_____.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,二次函数y=
x+2与x轴交于点A,与y轴交于点C,二次函数y=![]() x2+bx+c的图像经过A、C两点,与x轴的另一交点为点B.
x2+bx+c的图像经过A、C两点,与x轴的另一交点为点B.
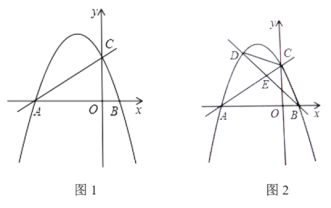
(1)求二次函数的表达式;
(2)当m≤x≤m1时,二次函数y![]() x2bxc的最大值为2m,求m的值;
x2bxc的最大值为2m,求m的值;
(3)如图2,点D为直线AC上方二次函数图像上一动点,连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1,△BCE的面积为S2,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com