
����Ŀ����ͼ����Rt��ABC�У���C=90����AC=2cm��AB=4cm����P�ӵ�A��������AB��1cm/s���ٶ����յ�B�˶�������P���A��B���غ�ʱ������P��PQ��AB������AC�ڵ�Q����AP��AQΪ�ڱ�������ƽ���ı���APMQ�����P���˶�ʱ��Ϊx��s��������������⣮
��1����A=�� ������
��2������M��BC��ʱ��x��ֵΪ�� ����
��3����ƽ���ı���APMQ����ABC���ص�����ͼ�ε����Ϊy��cm2������y��x֮��ĺ�����ϵʽ��
��4�������˶������У�ֱ��д����ABMΪֱ��������ʱx��ֵ��
���𰸡���1��60����2��![]() ����3��
����3��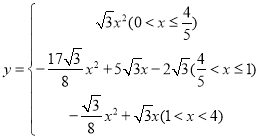 ����4��
����4��![]() ��2
��2
��������
��1�������A������ֵ���ɽ�����⣮
��2������ƽ���߷��߶γɱ�������������������⼴�ɣ�
��3�����������Σ���ͼ1�У���0��x��![]() ʱ���ص�������ƽ���ı���APMQ����ͼ3�У���
ʱ���ص�������ƽ���ı���APMQ����ͼ3�У���![]() ��x��1ʱ���ص������������APEFQ����ͼ4�У���1��x��4ʱ���ص��������ı���APEC���ֱ���⼴�ɽ�����⣮
��x��1ʱ���ص������������APEFQ����ͼ4�У���1��x��4ʱ���ص��������ı���APEC���ֱ���⼴�ɽ�����⣮
��4�����������Σ��ٵ���AMB=90�����������������ε����ʹ���������⣮�ڵ���ABM=90��ʱ�����������ε���λ�߶�����⼴�ɣ�
��1����ͼ�У�
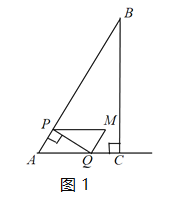
��Rt��ABC�У��ߡ�ACB=90����AC=2cm��AB=4cm��
��cosA=![]() ��
��
���A=60����
�ʴ�Ϊ��60��
��2����ͼ2�У�����M����BC��ʱ��
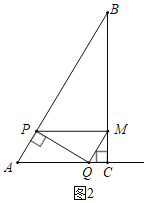
������֪��PA=xcm��
���ı���APMQ��ƽ���ı��Σ�
��PM=AQ=2AP=2x��
��PM��AC��
��![]() ��
��
��![]() ��
��
��x=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��3����ͼ1�У���0��x��![]() ʱ���ص�������ƽ���ı���APMQ��
ʱ���ص�������ƽ���ı���APMQ��
��Rt��APQ�У��ߡ�AQP=30����AP=x��
��AQ=2x��PQ=![]() x��
x��
��y=SAPMQ=AP��PQ=![]() x2��
x2��
��ͼ3�У���![]() ��x��1ʱ���ص������������APEFQ��AP=x��
��x��1ʱ���ص������������APEFQ��AP=x��
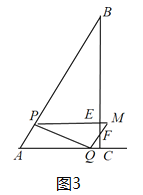
��AQ=PM=2x��PB=4��x��
��PE=![]() ��4��x����
��4��x����
��EM=PM��PE=2x��![]() ��4��x��=
��4��x��=![]() x��2��
x��2��
��EF=![]() ��
��![]() x��2����
x��2����
��y=SAPMQ��S��EFM=![]() x2��
x2��![]() ��
��![]() ��
��![]() x��2��2=��
x��2��2=��![]() x2+5
x2+5![]() x��2
x��2![]() ��
��
��ͼ4�У���1��x��4ʱ���ص��������ı���APEB��AP=x��

��AQ=2x��BP=4��x��
��PE=![]() ��4��x����
��4��x����
��BE=![]() ��4��x����
��4��x����
��CE=2![]() ��
��![]() ��4��x��=
��4��x��=![]() x��
x��
��y=S�ı���ACEP=![]() ��PE+AC��CE=
��PE+AC��CE=![]() [
[![]() ��4��x��+2]��
��4��x��+2]��![]() x=��
x=��![]() x2+
x2+![]() x��
x��
����������y= ��
��
��4����ͼ5�У�����AMB=90��ʱ����PQ��AM��F��
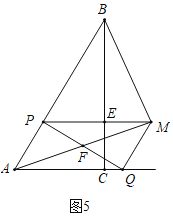
�ߡ�PAF=��BAM����APF=��AMB=90����
���APF�ס�AMB��
��![]() ��
��
��PA=x��PQ=![]() x��PF=FQ=
x��PF=FQ=![]() x��
x��
��AF=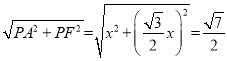 x��
x��
���ı���APMQ��ƽ���ı��Σ�
��AM=2AF=![]() x��
x��
��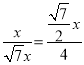 ��
��
��x=![]() ��
��![]() ����ȥ����
����ȥ����
��ͼ6�У�����ABM=90��ʱ����AM��PQ��F��
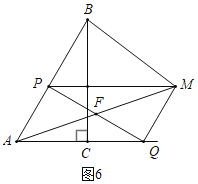
�ߡ�APF=��ABM=90����
��PF��BM��
��AF=FM��
��AP=PB=2��
��x=2��
��������������������x��ֵΪ![]() ��2��
��2��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��
��![]() ��
��![]() ��
��![]() ��������
��������![]() ��������
��������![]() ��
��![]() ����
����![]() �����н��ۣ�
�����н��ۣ�
��![]() ����
����![]() ��������
��������![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ����
����![]() .���н�����ȷ���У� ����
.���н�����ȷ���У� ����
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y=![]() x+2��x�ύ�ڵ�A����y�ύ�ڵ�C�����κ���y=
x+2��x�ύ�ڵ�A����y�ύ�ڵ�C�����κ���y=![]() x2+bx+c��ͼ��A��C���㣬��x�����һ����Ϊ��B��
x2+bx+c��ͼ��A��C���㣬��x�����һ����Ϊ��B��
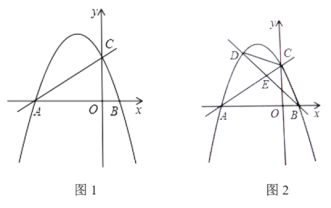
��1������κ����ı���ʽ��
��2����m��x��m1ʱ�����κ���y![]() x2bxc�����ֵΪ2m����m��ֵ��
x2bxc�����ֵΪ2m����m��ֵ��
��3����ͼ2����DΪֱ��AC�Ϸ����κ���ͼ����һ���㣬����BC��CD����ֱ��BD���߶�AC�ڵ�E����CDE�����ΪS1����BCE�����ΪS2����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90����BC��2����A��30��������ABC�Ƶ�C˳ʱ����ת120������PΪAB��һ���㣬��ת���P�Ķ�Ӧ��Ϊ��P'�����߶�PP'���ȵ���Сֵ�ǣ� ��
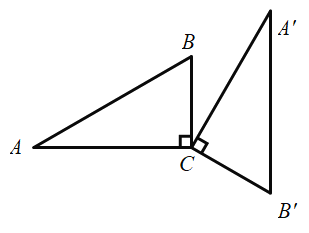
A.![]() B.2C.3D.2
B.2C.3D.2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʶ��
����Բ��ֱ���������˵��Բ��һ��Ϊ������������ǵ��������Σ���Բ����һ���Ϊ���Բ�ľ��ȵ㣮
����ѧ���⣩
��1����ͼ����AB����O��ֱ������PΪ��O��һ�㣬����AP����O�ڵ�C��PC��AC��
��֤����PΪ��O�ľ��ȵ㣮

��2����֪AB����O��ֱ������PΪ��O�ľ��ȵ㣬����AP����O�ڵ�C����PC��2AC����![]() ��ֵ��
��ֵ��
����������
��3����ͼ������֪AB����O��ֱ��������PΪ��O�ľ��ȵ㣬����AP����O�ڵ�C��PC��3AC������ֱ�ߺ�Բ�������������������ĵ�P����������ͼ�ۼ�����д������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
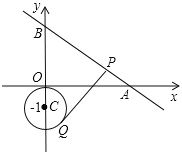
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����
����![]() ����
����![]() ΪԲ�ģ�1Ϊ�뾶��Բ��һ���㣬��Q������߽��߶�AB�ڵ�P�����߶�PQȡ��Сֵʱ��P���������__________��
ΪԲ�ģ�1Ϊ�뾶��Բ��һ���㣬��Q������߽��߶�AB�ڵ�P�����߶�PQȡ��Сֵʱ��P���������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼�������ڼ��ѧϰЧ����ij������ѧУҪ������˲��ԣ������ɼ��ֳ�![]() ����ȼ�������������ݻ������²�����ͳ��ͼ�����£��������⣺
����ȼ�������������ݻ������²�����ͳ��ͼ�����£��������⣺
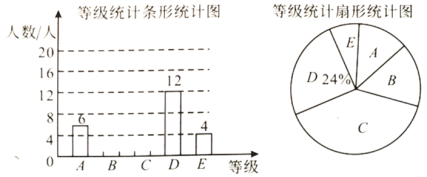
��1���ð������Ե�����Ϊ________��
��2��![]() �ȼ�������֮��Ϊ
�ȼ�������֮��Ϊ![]() ���������ݲ�ȫͳ��ͼ��
���������ݲ�ȫͳ��ͼ��
��3������ͼ�У�![]() �ȼ���������Ӧ������ͼ�е�Բ�Ľ�Ϊ________��
�ȼ���������Ӧ������ͼ�е�Բ�Ľ�Ϊ________��
��4����ȫ�꼶����1400�ˣ�������꼶�����Եȼ���![]() �ȼ����ϣ�����
�ȼ����ϣ�����![]() ������ѧ��������
������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
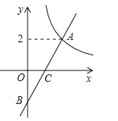
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У�һ�κ���y=kx-k��ͼ���뺯��y=![]() (x��0)��ͼ��ΪA����y�ύ�ڵ�B��P��x����һ�㣬����PAB�������4����P������____��
(x��0)��ͼ��ΪA����y�ύ�ڵ�B��P��x����һ�㣬����PAB�������4����P������____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��֯Ա���������ľ������Σ������������ṩ���շѷ�������������ͼ��ʾ��ͼ��ͼ������ABCD��ʾ�˾��շ�y��Ԫ����μ����ε�����x���ˣ�֮��ĺ�����ϵ��
��1�����μ����ε�����������10��ʱ���˾��շ�Ϊ�� ��Ԫ��
��2������ù�˾֧����������3600Ԫ����ô�μ�������ε������Ƕ��٣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com