
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,
,
(1)求证:对任意的实数![]() ,函数
,函数![]() 与
与![]() 的图象总有两个交点;
的图象总有两个交点;
(2)设![]() 与
与![]() 的图象相交于
的图象相交于![]() 两点,
两点,![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,记
,记![]() 与
与![]() 的面积分别为
的面积分别为![]() (
(![]() 为坐标原点),求证:
为坐标原点),求证:![]() 总是定值;
总是定值;
(3)对于二次函数![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,恰好有
时,恰好有![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)把两函数联立得到一元二次方程,根据根的判别式△>0即可求解;
(2)设![]() ,根据一元二次方程根与系数的关系得到
,根据一元二次方程根与系数的关系得到![]() ,再根据二次函数的解析式求出C点坐标,得到
,再根据二次函数的解析式求出C点坐标,得到![]() ,再代入
,再代入![]() 即可求解;
即可求解;
(3)先把二次函数化为顶点式,当![]() 时,
时,![]() 有最大值
有最大值![]() ,根据当
,根据当![]() 时,恰好有
时,恰好有![]() ,故
,故![]() ,而函数的对称轴为
,而函数的对称轴为![]() ,得到函数值会随着
,得到函数值会随着![]() 增大而增大,把(a,a)和(b,b)代入二次函数,再根据根与系数的关系得到
增大而增大,把(a,a)和(b,b)代入二次函数,再根据根与系数的关系得到![]() ,故可求出
,故可求出![]() 的值.
的值.
解:(1)联立![]() 与
与![]() 的方程
的方程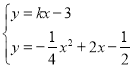
消去![]() 得
得![]()
![]()
![]() 对任意的实数
对任意的实数![]() ,函数
,函数![]() 与
与![]() 的图象总有两个交点.
的图象总有两个交点.
(2)设![]() ,则
,则![]() 是方程
是方程![]() 的两根,
的两根,
由根与系数的关系知:![]() ,因为二次函数
,因为二次函数![]() 与
与![]() 轴相交于点
轴相交于点![]()
所以![]()
故![]() 总是定值
总是定值![]() ;
;
(3)![]() ,当
,当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
所以![]() ,而函数的对称轴为
,而函数的对称轴为![]() ,
,
所以当![]() 时,
时,
函数值会随着![]() 增大而增大,
增大而增大,
把(a,a)和(b,b)代入二次函数得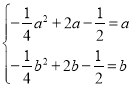 ,
,
则
所以![]() 是方程
是方程![]() 的两根且这两根均小于4,
的两根且这两根均小于4,
所以![]()
∴ .
.


科目:初中数学 来源: 题型:
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
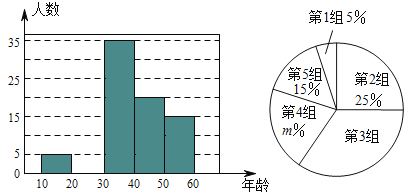
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5μm(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为
A.25×10﹣7B.2.5×10﹣6C.0.25×10﹣5D.2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与![]() 轴交于
轴交于![]() ,
,![]() 点,与
点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,连接
,连接![]() .
.
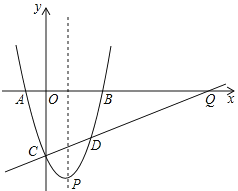
(1)求此抛物线的表达式;
(2)在抛物线上找一点![]() ,使得
,使得![]() 与
与![]() 垂直,且直线
垂直,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)抛物线对称轴上是否存在一点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,二次函数y=
x+2与x轴交于点A,与y轴交于点C,二次函数y=![]() x2+bx+c的图像经过A、C两点,与x轴的另一交点为点B.
x2+bx+c的图像经过A、C两点,与x轴的另一交点为点B.
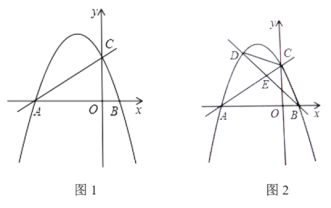
(1)求二次函数的表达式;
(2)当m≤x≤m1时,二次函数y![]() x2bxc的最大值为2m,求m的值;
x2bxc的最大值为2m,求m的值;
(3)如图2,点D为直线AC上方二次函数图像上一动点,连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1,△BCE的面积为S2,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):
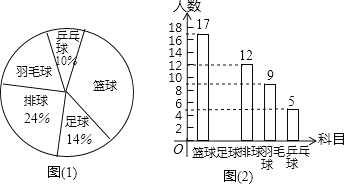
(1)请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);
(2)在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC=2,∠A=30°,将△ABC绕点C顺时针旋转120°,若P为AB上一动点,旋转后点P的对应点为点P',则线段PP'长度的最小值是( )
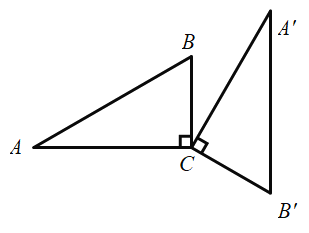
A.![]() B.2C.3D.2
B.2C.3D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ;点
;点![]() 是以
是以![]() 为圆心,1为半径的圆上一动点,过Q点的切线交线段AB于点P,当线段PQ取最小值时,P点的坐标是__________.
为圆心,1为半径的圆上一动点,过Q点的切线交线段AB于点P,当线段PQ取最小值时,P点的坐标是__________.
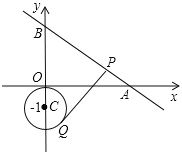
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com