
【题目】如图1,将两根笔直的细木条![]() 用图钉固定并平行摆放,将一根橡皮筋拉直后用图有分别周定在
用图钉固定并平行摆放,将一根橡皮筋拉直后用图有分别周定在![]() 上,橡皮筋的两端点分别记为点
上,橡皮筋的两端点分别记为点![]() ,点
,点![]() .
.
(1)图1中,点![]() 在
在![]() 上,若
上,若![]() ,则
,则![]() ___________
___________![]() ;
;
(2)![]() 为橡皮筋上一点,,用橡皮筋的弹性拉动橡皮筋,使
为橡皮筋上一点,,用橡皮筋的弹性拉动橡皮筋,使![]() 三点不在同一直线,后用图固定点
三点不在同一直线,后用图固定点![]() .
.
①如图2,若点![]() 在两根细木条所在直线之间,且
在两根细木条所在直线之间,且![]() ,试判断线段
,试判断线段![]() 与
与![]() 所在直线的位置关系,并说明理由;
所在直线的位置关系,并说明理由;
②如图3,若点![]() 在两根细木条所在直线的同侧,且
在两根细木条所在直线的同侧,且![]() ,
,![]() ,试求
,试求![]() 的度数;
的度数;
(3)如图4,![]() 为AB上两点,拉动橡皮筋并固定,若
为AB上两点,拉动橡皮筋并固定,若![]() ,则
,则![]() ____________
____________![]() .
.
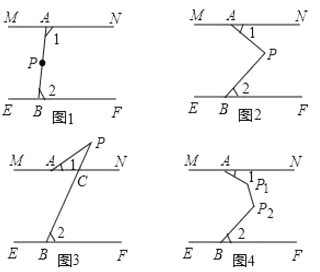
【答案】(1) 70;(2)①AP⊥BP,理由见解析;②∠1=31°,∠2=59° (3) 270.
【解析】
(1)根据MN∥EF即可得出∠1+∠2=180°,结合∠1=110°即可求出∠2的度数;
(2)①过点P作PC∥MN,根据MN∥EF即可得出PC∥MN∥EF,进而得出∠APC=∠1,∠BPC=∠2再根据角与角之间的关系即可得出∠APB=∠1+∠2=90°,由此即可得出AP⊥BP;
②2过点P作PD∥MN,同理可得出∠APC=∠1,∠BP=∠2,根据角与角之间的关系即可得出∠APB=∠2-∠1=28°,再结合∠1+∠2=90°,即可求出∠1、∠2的度数;
(3)过点P作P1C∥MN,过点P2作P2D∥MN,由MN∥EF即可得出P1c∥MN∥EF∥P2D,从而可得出∠1=∠AP1C,∠2=∠BP2D,∠CP1P2+∠DP2P1=180°,再根据角与角之间的关系即可算出∠AP1P2+∠BP2P1的度数.
(1)∵MN∥EF,
∴∠1+∠2=180°,
∵∠1=110°,
∴∠2=70°
故答案为:70.
(2)①AP⊥BP,理由如下
在图2中,过点P作PC∥MN,
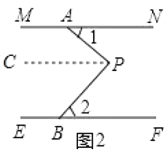
∵MN∥EF,
∴PC∥MN∥EF,
∴∠APC=∠1,∠BPC=∠2.
∵∠APB=∠APC+∠BPC,∠1+∠2=90°,
∴∠APB=90°,
∴AP⊥BP.
②在图3中,过点P作PD∥MN,
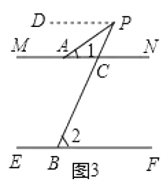
∵MN∥EF,
∴PD∥MN∥EF,
∴∠DPA=∠1,∠DPB=∠2,
∴∠APB=∠DPB-∠DPA=∠2-∠1=28°
又∵∠1+∠2=90°,
∴∠1=31°,∠2=59°
(3)在图4中,过点P作PC∥MN,过点P2作P2D∥MN,
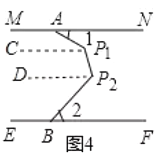
∵MN∥EF,
∴P1C∥MN∥EF∥P2D,
∴∠1=∠AP1C,∠2=∠BP2D,∠CP1P2+∠DP2P1=180°,
又∵∠1+∠2=90°,
∴∠AP1P2+∠BP2P1=∠AP1C+∠CP1P2+∠BP2D+∠BP2P1
=(∠AP1C+∠BP2D)+( ∠CP1P2+∠DP2P1)=90°+180°=270°
故答案为:270.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题
《九章算术》是中国古代第一部数学专著,也是世界上最早的印刷本数学书它的出现标志着中国古代数学体系的形成.《九章算术》早在隋唐时期即已传入朝鲜、日本并被译成日、俄、德、法等多种文字版本.书中有如下问题:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?
大意是:有几个人一起去买一件物品,如果每人出8元,则多了3元;如果每人出7元,则少了4元钱,问有多少人?该物品价值多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,点E是BC的中点,连接DE,DF⊥DE交BA的延长线于点F.连接EF、AC,DE、EF分别与C交于点P、Q,则PQ=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B. 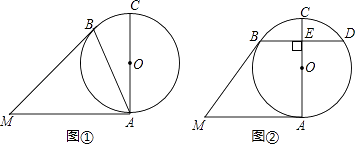
(1)如图①,若∠BAC=23°,求∠AMB的大小;
(2)如图②,过点B作BD∥MA,交AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.
(1)若CB=4,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC;
小洁在遇到此问题时不知道怎么下手,秦老师提示他可以过点C作CH![]() CF,交DB于点H,先证明△AFC
CF,交DB于点H,先证明△AFC![]() △BHC,然后继续思考,并鼓励小洁把证明过程写出来.请你帮助小洁完成这个问题的证明过程.
△BHC,然后继续思考,并鼓励小洁把证明过程写出来.请你帮助小洁完成这个问题的证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com