
����Ŀ�����ش������ֺͷ�չ������ҵ��A��B��C����������֮���λ�ù�ϵ��ͼ1��ʾ����֪B��������A����������������50���ﴦ��C��������A����������������50���ﴦ��A��������1��ֻ����B����������ֳ������������ֳ��������ֳ����50%��C�������������ּ�������ͬѧ��������������ֳ�����Ƴ���ͼ2��ʾ�IJ�����������ͳ��ͼ����C���������ּ�����ֳ�����Ƴ���ͼ3��ʾ������ͳ��ͼ��
��1����ȫͼ2�е�����ͳ��ͼ��
��2�����ڹǼ������������Ƽ����Ե����ε�Բ�ĽǵĶ�����
��3���������ž�����B��C���е㽨��һ��������ת����E���Խ�������������ļ����������⣬��֪A��B��C������������ÿֻ������ƽ��������Ϊ1�䣬������һ�伦��ÿ����ķ��ö�Ϊ0.5Ԫʱ�����A��B��C�������������伦����������ת����Eһ����ܷ���Ϊ����Ԫ������ʾ�� ![]() =1.4��
=1.4��

���𰸡���1����ȫ����ͳ��ͼ��������
��2�������ּ���������1600ֻ�����������Ե����ε�Բ�ĽǵĶ�����126�㣻
��3����A��B��C�������������伦����������ת����Eһ����ܷ���Ϊ700000Ԫ��
�������������������1�����������ȥA��B�����������ļ������ɵõ������
��2���������Ժ����ּ���ռ�İٷֱȼ��ɵõ������ּ���������360�����Ժ�������ռ�İٷֱȼ��ɵõ����������Ե����ε�Բ�ĽǵĶ�����
��3��Ҫ�ƽ��˷ѣ�����Ҫ���AE��BE��CE�ij���Ȼ����ý����
���������
��1��C�������ļ���2��50%��1��2=1��ֻ����ͼ��ȫͼ2�е�����ͳ��ͼ��
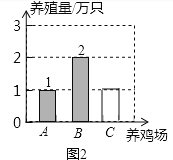
��2��40000����1��35%��25%��=1600ֻ��360���35%=126����
�𣺺����ּ���������1600ֻ�����������Ե����ε�Բ�ĽǵĶ�����126����
��3����Rt��ABC�У�AB=AC=50��E��BC���е㣬
��AE=CE=BE=25![]() ��
��
��40000��1��0.5��25![]() =700000Ԫ��
=700000Ԫ��
�𣺴�A��B��C�������������伦����������ת����Eһ����ܷ���Ϊ700000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ���õ���ʮ���ƣ���:1967=1��103+9��102+6��101+7����ʾʮ���Ƶ���Ҫ��10�����룺0��1��2��3��4��5��6��7��8��9���ڼ�������õ��Ƕ����ƣ�ֻ���������룺0��1����:��������111=1��22+1��21+1�൱��ʮ�����е�7�����磺11011=1��24+1��23+0��22+1��21+1�൱��ʮ�����е�27����ô�������е�1011�൱��ʮ�����е�( )
A. 9B. 10C. 11D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ǶԶ��ǣ������IJ�����100�������������ǵĶ�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A��B������Ʒ����2��A��Ʒ��1��B��Ʒ����90Ԫ����3��A��Ʒ��2��B��Ʒ������160Ԫ.
��1����A��B������Ʒÿ������Ԫ��
��2�����С��������A��B������Ʒ��10�����ܷ��ò�����350Ԫ���Ҳ�����300Ԫ�����м��ֹ��������ַ���������ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ε����Ʊ�Ϊ2��5���ܳ���Ϊ12���ף���ϴ������ε��ܳ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊ1��С��������ɵķ���ֽ�У���С�����εĶ���Ϊ�������������ȫ�ڸ���ϵĶ����Ϊ�����������.������ε������ΪS�����ڲ��ĸ������ΪN���߽��ϵĸ������ΪL�����磬ͼ�е�������ABC�Ǹ�������Σ�����S=2��N=0��L=6��ͼ�и������DEFGHI����Ӧ��S��N��L�ֱ��� _.��̽�����֣����������ε����S�ɱ�ʾΪS=aN+bL+c������a��b��cΪ��������N=5��L=14ʱ��S= .������ֵ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y��![]() ��x��0����ͼ������һ��A��m��4��������A��AB��x���ڵ�B������B����ƽ��2����λ���ȵõ���C������C��y���ƽ���߽�������������ͼ���ڵ�D��CD��
��x��0����ͼ������һ��A��m��4��������A��AB��x���ڵ�B������B����ƽ��2����λ���ȵõ���C������C��y���ƽ���߽�������������ͼ���ڵ�D��CD��![]() ��
��
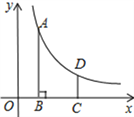
��1�����D�ĺ����꣨�ú�m��ʽ�ӱ�ʾ����
��2�����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1������3a2b3��2����a3b2��5��a2b4��
��2���� ![]() ��2012������1.5��2013�£���1��2014��
��2012������1.5��2013�£���1��2014��
��3��[x��x2y2��xy����y��x2��x3y��]��3x2y��
��4����5x+7y��3����5x��7y+3����
��5����a+2b��c��2��
��6����x+2y��2��x��2y��2 ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com