Question

【题目】小明和哥哥在环形跑道上练习长跑．他们从同一起点沿相反方向同时出发，每隔25秒钟相遇一次．现在，他们从同一起跑点沿相同方向同时出发，经过25分钟哥哥追上了小明，并且比小明多跑了20圈，求：

（1）哥哥速度是小明速度的多少倍？

（2）哥哥追上小明时，小明跑了多少圈？

Answer 1

【答案】（1）哥哥速度是小明速度的2倍；（2）20圈．

【解析】（1）由“他们从同一起点沿相反方向同时出发，每隔25秒钟相遇一次”得到等量关系：哥哥所跑路程+小明所跑路程=环形跑道的周长；由“经过25分钟哥哥追上小明，并且比小明多跑了20圈”，知经过分钟哥哥追上小明，并且比小明多跑了1圈，得到等量关系：哥哥所跑路程-小明所跑路程=环形跑道的周长，据此列出方程组，求出问题的解．
（2）由（1）中求出的哥哥的速度与小明的速度的比为2：1，可知在时间相同时，他们所行的路程比也为2：1．如果设小明跑了x圈，那么哥哥跑了2x圈．根据哥哥比小明多跑了20圈列式解答即可．

解：设哥哥的速度是V1米/秒，小明的速度是V2米/秒．环形跑道的周长为s米．

（1）由题意，有，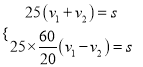

整理得，4v2=2v1，

所以，V1=2V2．

答：哥哥速度是小明速度的2倍．

（2）设小明跑了x圈，那么哥哥跑了2x圈．

根据题意，得2x﹣x=20，

解得，x=20．

故经过了25分钟小明跑了20圈．

“点睛”本题考查分式方程、一元一次方程的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．本题要注意追及问题和相遇问题不同的求解方法及时间相同，路程比等于速度比．