
 如图,已知⊙O的半径为1,AB、CD都是它的直径,∠AOD=60°,点P在劣弧
如图,已知⊙O的半径为1,AB、CD都是它的直径,∠AOD=60°,点P在劣弧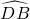 上运动变化.
上运动变化. ∠AOC,
∠AOC, ×120°=60°,
×120°=60°,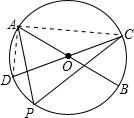 ∵∠AOD=60°,OA=OD
∵∠AOD=60°,OA=OD ,
,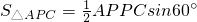 ,
,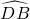 上运动,则点P到AC的距离是变化的,底边AC为定值,
上运动,则点P到AC的距离是变化的,底边AC为定值,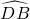 的中点时,点P到AC的距离的最大.
的中点时,点P到AC的距离的最大. ×
× =
= ,
, .
.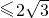 .
. ∠AOC,而∠AOC=180°-60°=120°,所以∠APC=
∠AOC,而∠AOC=180°-60°=120°,所以∠APC= ×120°=60°.
×120°=60°. ,在△APC中,由余弦定理得:AC2=AP2+PC2-2APPCcos60°,变形为(AP+PC)2=3+3AP•PC,然后由
,在△APC中,由余弦定理得:AC2=AP2+PC2-2APPCcos60°,变形为(AP+PC)2=3+3AP•PC,然后由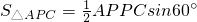 ,以及三角形APC的面积等于AC与P到AC的距离的一半得到AP•PC是变化的,当点P为
,以及三角形APC的面积等于AC与P到AC的距离的一半得到AP•PC是变化的,当点P为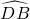 的中点时,可分析出并求出PA+PC的最大值为
的中点时,可分析出并求出PA+PC的最大值为 ;当点P与点D或点B重合,可分析出并求出PA+PC的最小值为3,由此得到PA+PC值的变化范围.
;当点P与点D或点B重合,可分析出并求出PA+PC的最小值为3,由此得到PA+PC值的变化范围.

科目:初中数学 来源: 题型:
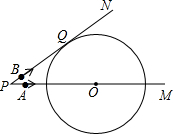 P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.
P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:
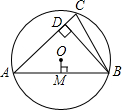 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A、0.6 | B、0.8 | C、0.5 | D、1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:
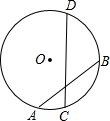 如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )
如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com