Question

17．某一蓄水池中有水若干吨，若单一个出水口，排水速度v（m³/h）与排完水池中的水所用的时间t（h）之间的对应值关系如下表：

排水速度 （m3/h）	1	2	3	4	6	8	12
所用的时间 t（h）	12	6	4	3	2	1.5	1

（1）在如图的直角坐标系中，用描点法画出相应函数的图象；
（2）写出t与v之间的函数关系式；
（3）若5h内排完水池中的水，那么每小时的排水量至少应该是多少？

Answer 1

分析 （1）根据表格中所有数对确定点的坐标，利用描点法作图即可；
（2）根据th=12确定两个变量之间的函数关系即可；
（3）根据0＜t≤5时，0＜v≤2.4，从而确定最小排出量即可．

解答 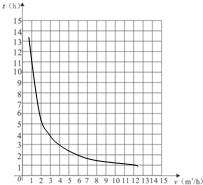解：（1）函数图象如图所示．…2分
   （2）根据图象的形状，选择反比例函数模型进行尝试．
设v=$\frac{k}{t}$（k≠0），选（1，12）的坐标代入，得k=12，
∴v=$\frac{12}{t}$．
∵其余点的坐标代入验证，符合关系式v=$\frac{12}{t}$．
∴所求的函数解析式是v=$\frac{12}{t}$（t＞0）．
  （3）由题意得：当0＜t≤5时，v≥2.4．即每小时的排水量至少应该是2.4m³．

点评 本题考查了反比例函数的应用，现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式，再运用函数关系式解题．