
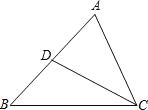
【题目】如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=![]() ,求:
,求:
(1)△ABC的面积;
(2)sin∠ACD的值.
【答案】(1)6;(2)![]() .
.
【解析】
试题分析:(1)作AH⊥BC于H,如图,在Rt△ACE中,利用正切的定义得到tan∠ACE=![]() =3,则设CH=x,AH=3x,根据勾股定理得AC=
=3,则设CH=x,AH=3x,根据勾股定理得AC=![]() x,利用
x,利用![]() x=
x=![]() ,解得x=1,再在Rt△ABH中,利用∠B=45°得到BH=AH=3,然后根据三角形面积公式求解;
,解得x=1,再在Rt△ABH中,利用∠B=45°得到BH=AH=3,然后根据三角形面积公式求解;
(2)作DF⊥BC于F,如图,由于CD是AB边上的中线,根据三角形面积公式得到S△ACD=S△ABC=6,再证明DF为△AB的中位线,则DF=![]() AH=
AH=![]() ,易得BF=DF=
,易得BF=DF=![]() ,接着根据勾股定理计算出CD=
,接着根据勾股定理计算出CD=![]() ,然后利用锐角三角函数得出sin∠ACD的值.
,然后利用锐角三角函数得出sin∠ACD的值.
试题解析:(1)如图,
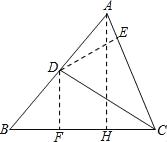
(1)作AH⊥BC于H,
在Rt△ACH中,
∵tan∠ACB=3,AC=![]() ,
,
设CH=x,AH=3x,
根据勾股定理得AC=![]() x,
x,
∴CH=1,AH=3,
在Rt△ABH中,∠B=45°,
∴BH=AH=3,
∴S△ABC=![]() ×4×3=6;
×4×3=6;
(2)作DF⊥BC于F,
∵S△ACD=![]() ×
×![]() ×DE=3,
×DE=3,
∴DE=![]() ,
,
∵AH⊥BC,DF⊥BC,CD是AB边上的中线,
∴DF=![]() AH=
AH=![]() ,
,
∴BF=DF=![]() ,
,
在Rt△CDF中,CD=![]() ,
,
∴在Rt△CDE中,sin∠ACD=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数的乘方:求n个________因数的积的运算,叫做乘方,乘方的结果叫做________.在an中,a叫做________,n叫做________,读作________或________;表示的意义为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具有绿色低碳、方便快捷、经济环保等特点的共享单车行业近几年蓬勃发展,我国2017年全年共享单车用户达6170万人.将数据“6170万”用科学记数法表示为( )
A. 6.17×103 B. 6.17×105 C. 6.17×107 D. 6.17×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物指数如表,则该周PM2.5指数的众数和中位数分别是________
PM2.5指数 | 150 | 155 | 160 | 165 |
天 数 | 3 | 2 | 1 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com