
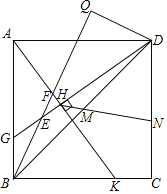
【题目】如图,Q为正方形ABCD外一点,连接BQ,过点D作DQ⊥BQ,垂足为Q,G、K分别为AB、BC上的点,连接AK、DG,分别交BQ于F、E,AK⊥DG,垂足为点H,AF=5,DH=8,F为BQ中点,M为对角线BD的中点,连接HM并延长交正方形于点N,则HN的长为_____.
【答案】![]()
【解析】
由于M是对角线BD中点,因此连接AC,则AC必过M点,且A、H、M、D四点共圆,从而∠DHM=∠MAD=45°,作NP⊥DH于P,则PH=NP,△NPD与△DHA相似,因此只要知道AH与DH之比就可以解决问题了.而DH已知,AF已知,只需求出FH即可.作BR⊥AK于R,连接MR,MF,作MO⊥HR于O,注意到F为BQ中点,于是FM是中位线,由A、M、R、B四点共圆可得△MHR是等腰直角三角形,于是MO=HO=OR,结合△MFO~△FBR,△ABR≌△DAH得到的等量关系可以解出HF的长度,从而求得HN的长度.
连接AC,则AC必过BD中点M.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ADC=90°,
作BR⊥AK于R,连接MR,

则∠ABR+∠BAR=∠BAR+∠DAH=90°,
∴∠ABR=∠DAH,
∵DG⊥AK于H,
∴∠DHA=∠ARB=90°,
在△ABR和△DAH中:
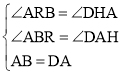
∴△ABR≌△DAH(AAS),
∴BR=AH,AR=DH,
∵正方形对角线AC、BD交于点M,
∴AM=BM=DM,∠BMA=∠AMD=90°,∠MBA=∠MAB=∠MAD=∠MDA=45°,
∴∠BRA=∠BMA,∠AHD=∠AMD,
∴A、B、R、M四点共圆,A、H、M、D四点共圆,
∴∠ARM=∠ABM=45°,∠DHM=∠DAM=45°,
∴∠RHM=∠RHD﹣∠DHM=90°﹣45°=45°,
∴∠RHM=∠HRM=45°,
∴△HMR是等腰直角三角形,
∴OM=OH=OR,
作MO⊥HR,则HO=OR,连接FM,
∵F为BQ中点,
∴FM为△BDQ的中位线,
∴FM∥DQ,
∵DQ⊥BQ,
∴FM⊥BQ,
∴∠BFM=∠BFR+MFO=90°,
又∵∠BFR+∠FBR=90°,
∴∠FBR=∠MFO,
∵∠MOF=∠FRB=90°,
∴△BFR△FMO,
∴![]() =
=![]() ,
,
设FH=x,OM=OH=OR=y,
∵AF=5,DH=8,
∴BR=AH=AF+FH=5+x,AR=DH=AF+FR=5+x+2y=8,
∴FR=x+2y=3,
∴![]() =
=![]() ,
,
解得:x=y=1,
∴AH=AF+x=6,
作NP⊥DG于P,则∠PND+∠PDN=∠PDN+∠ADH=90°,
∴∠ADH=∠PND,
∵∠AHD=∠DPN=90°,
∴△AHD△DPN,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
设PD=3k,PN=4k,
又∵∠DHM=45°,
∴△HPN是等腰直角三角形,
∴PH=PN=4k,HN=![]() PH=4
PH=4![]() k,
k,
∵DH=PD+PH=3k+4k=7k=8,
∴k=![]() ,
,
∴HN=![]() .
.
故答案为:![]() .
.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() (圆心
(圆心![]() 在
在![]() 内部)经过
内部)经过![]() 两点,交线段
两点,交线段![]() 于点
于点![]() 直径
直径![]() 交
交![]() 于点
于点![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 上.连结
上.连结![]() .
.
![]() 求证:
求证:![]() .
.
![]() 在圆心
在圆心![]() 的运动过程中,
的运动过程中,
![]() 若
若![]() ,求
,求![]() 的长.
的长.
![]() 若点
若点![]() 关于
关于![]() 的对称点落在
的对称点落在![]() 边上时,求
边上时,求![]() 的值.(直接写出答案)
的值.(直接写出答案)
![]() 令
令![]() 与边
与边![]() 的另一个交点为
的另一个交点为![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() 若
若![]() ,垂足为点
,垂足为点![]() 求证:
求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a=____,b=_____,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计跳绳能够一分钟完成160或160次以上的学生有多少人?
(3)已知第一组中有两个甲班学生,第四组中只有一个甲班学生,老师随机从这两个组中各选一名学生谈测试体会,则所选两人正好都是甲班学生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
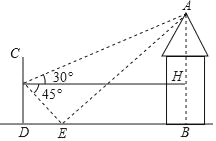
【题目】为了测量休闲凉亭AB的高度,某数学兴趣小组在水平地面D处竖直放置一个标杆CD,并在地面上水平放置一个平面镜E,使得B、E、D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到凉亭顶端A,在F处测得凉亭A顶端的仰角为30°,平面镜E的俯角为45°,FD=2米,求休闲凉亭AB的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,线段AC是⊙O的直径,过A点作直线BF交⊙O于A、B两点,过A点作∠FAC的角平分线交⊙O于D,过D作AF的垂线交AF于E.
(1)证明DE是⊙O的切线;
(2)证明AD2=2AEOA;
(3)若⊙O的直径为10,DE+AE=4,求AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB
外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.

(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
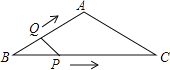
A.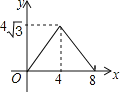 B.
B.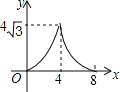
C.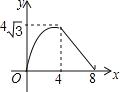 D.
D.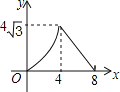
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com