
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

科目:初中数学 来源: 题型:
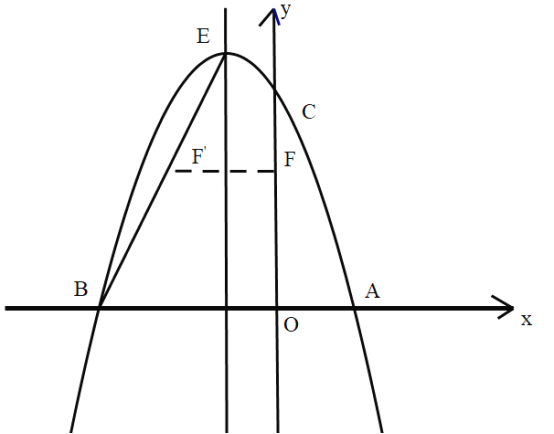
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线l是抛物线的对称轴,
,直线l是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)如图,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
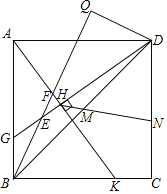
【题目】如图,Q为正方形ABCD外一点,连接BQ,过点D作DQ⊥BQ,垂足为Q,G、K分别为AB、BC上的点,连接AK、DG,分别交BQ于F、E,AK⊥DG,垂足为点H,AF=5,DH=8,F为BQ中点,M为对角线BD的中点,连接HM并延长交正方形于点N,则HN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
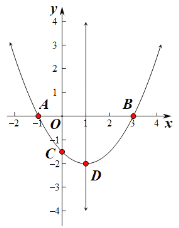
【题目】抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,交
,交![]() 轴的负半轴于
轴的负半轴于![]() ,顶点为
,顶点为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④当
;④当![]() 是等腰直角三角形时,则
是等腰直角三角形时,则![]() ;⑤若
;⑤若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两个根,且
的两个根,且![]() ,则
,则![]() .其中错误的有( )个.
.其中错误的有( )个.
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某商品的进价为每件40元.现在的售价是每件60元.每星期可卖出300件.市场调查反映:如调整价格,每涨价一元.每星期要少卖出10件;每降价一元,每星期可多卖出18件.如何定价才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 是一张放在平面直角坐标系中的纸片,点
是一张放在平面直角坐标系中的纸片,点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上.已知
轴的正半轴上.已知![]() ,
,![]() .将纸片的直角部分翻折,使点
.将纸片的直角部分翻折,使点![]() 落在
落在![]() 边上,记为点
边上,记为点![]() ,
,![]() 为折痕,点
为折痕,点![]() 在
在![]() 轴上.
轴上.

(1)在如图所示的直角坐标系中,点![]() 的坐标为,________,
的坐标为,________,![]() ________;
________;
(2)线段![]() 上有一动点
上有一动点![]() (不与点
(不与点![]() ,
,![]() 重合)自点
重合)自点![]() 沿
沿![]() 方向以每秒
方向以每秒![]() 个单位长度向点
个单位长度向点![]() 做匀速运动,设运动时间为
做匀速运动,设运动时间为![]()
![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积
的面积![]() 与时间
与时间![]() 之间的函数表达式.当
之间的函数表达式.当![]() 取何值时,
取何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
(3)当![]()
![]() 为何值时,
为何值时,![]() ,
,![]() ,
,![]() 三点构成一个等腰三角形?并求出点
三点构成一个等腰三角形?并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
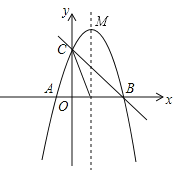
(1)求该抛物线的表达式;
(2)点![]() 是线段
是线段![]() 上方的抛物线上一个动点,求
上方的抛物线上一个动点,求![]() 的面积的最大值;
的面积的最大值;
(3)点![]() 是抛物线的对称轴上一个动点,当以
是抛物线的对称轴上一个动点,当以![]()
![]()
![]() 为顶点的三角形是直角三角形时,求出点
为顶点的三角形是直角三角形时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
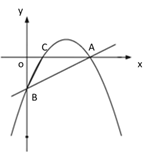
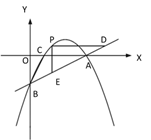
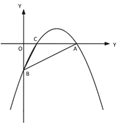
① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇在“精准扶贫”活动中销售农产品,经分析发现月销售量![]() (万件与月份
(万件与月份![]() (月)的关系为:
(月)的关系为: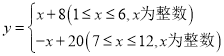
每件产品的利润![]() (元)与月份
(元)与月份![]() (月)的关系如下表:
(月)的关系如下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
![]() 请你根据表格直接写出每件产品利润z (元) 与月份
请你根据表格直接写出每件产品利润z (元) 与月份![]() (月)的函数关系式;
(月)的函数关系式;
![]() 若月利润
若月利润![]() (万元) =当月销售量
(万元) =当月销售量![]() (万件)
(万件) ![]() 当月每件产品的利润
当月每件产品的利润![]() (元),求月利润
(元),求月利润![]() (万元)与月份
(万元)与月份![]() (月)的关系式;
(月)的关系式;
![]() 当
当![]() 为何值时,月利润
为何值时,月利润![]() 有最大值,最大值为多少?
有最大值,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com