
【题目】抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,交
,交![]() 轴的负半轴于
轴的负半轴于![]() ,顶点为
,顶点为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④当
;④当![]() 是等腰直角三角形时,则
是等腰直角三角形时,则![]() ;⑤若
;⑤若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两个根,且
的两个根,且![]() ,则
,则![]() .其中错误的有( )个.
.其中错误的有( )个.
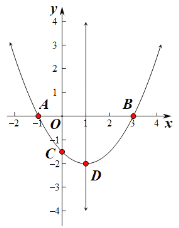
A.5B.4C.3D.2
【答案】B
【解析】
根据二次函数图象与系数的关系,可知![]() ,故
,故![]() ,①正确;将A、B两点代入可得c、b的关系,可判定②;函数开口向上,
,①正确;将A、B两点代入可得c、b的关系,可判定②;函数开口向上,![]() 时取得最小值,则
时取得最小值,则![]() ,
,![]() 可判断
可判断![]() ,故③不正确;根据图象
,故③不正确;根据图象![]() ,顶点坐标,判断
,顶点坐标,判断![]() ;根据题意,二次函数化为交点式是
;根据题意,二次函数化为交点式是![]() ,令y=4,结合图像可知,
,令y=4,结合图像可知,![]() ,可以判断⑤.
,可以判断⑤.
①:根据二次函数图象与系数的关系,可知![]() ,
, ![]() ,故①正确;
,故①正确;
![]() 二次函数
二次函数![]() 与x轴交于点
与x轴交于点![]() 、
、![]() .即得二次函数的对称轴为
.即得二次函数的对称轴为![]() ,即
,即![]() ,
,![]()
![]() ,
,![]() .
.
又![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() .
.
故![]() 错误;
错误;
![]() 抛物线开口向上,对称轴是
抛物线开口向上,对称轴是![]() .
.
![]() 时,二次函数有最小值.
时,二次函数有最小值.
![]() 时,
时,![]() .
.
即![]() .
.
故![]() 不正确;
不正确;
![]() ,
,![]() ,若
,若![]() 是等腰直角三角形.
是等腰直角三角形.
![]() .
.
解得,![]() .
.
设点D坐标为![]() .
.
则![]() .
.
解得![]() .
.
![]() 点D在x轴下方.
点D在x轴下方.
![]() 点D为
点D为![]() .
.
![]() 二次函数的顶点D为
二次函数的顶点D为![]() ,过点
,过点![]() .
.
设二次函数解析式为![]() .
.
![]() .
.
解得![]() .
.
故![]() 不正确;
不正确;
⑤:根据题意,二次函数化为交点式是![]() ,令y=4,结合图像可知,
,令y=4,结合图像可知,![]() ,也即一元二次方程
,也即一元二次方程![]() 的两个根
的两个根![]() ,故⑤不正确.
,故⑤不正确.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,线段AC是⊙O的直径,过A点作直线BF交⊙O于A、B两点,过A点作∠FAC的角平分线交⊙O于D,过D作AF的垂线交AF于E.
(1)证明DE是⊙O的切线;
(2)证明AD2=2AEOA;
(3)若⊙O的直径为10,DE+AE=4,求AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB
外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.

(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
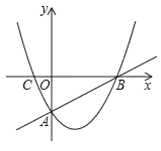
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求抛物线的解析式;
(2)![]() 为抛物线上一点,直线
为抛物线上一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在直线![]() 下方的抛物线上是否存在点
下方的抛物线上是否存在点![]() ,使得
,使得![]() ,如果存在这样的点
,如果存在这样的点![]() ,请求出点
,请求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建造一个面积为130m2的长方形养鸡场,鸡场的一边靠墙,墙长为a米,另三边用竹篱笆围成,如果篱笆总长为33米.
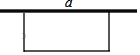
(1)求养鸡场的长与宽各为多少米?
(2)若10≤a<18,题中的解的情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=3,AB=4,则四边形AEDF的周长为( )
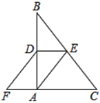
A.8B.9C.10D.11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com