练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠BAC=90°，D、E分别是AB、BC的中点，F在CA延长线上，∠FDA=∠B，AC=3，AB=4，则四边形AEDF的周长为（ ）

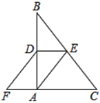
    A.8B.9C.10D.11

    【答案】A

    【解析】

    根据勾股定理先求出BC的长，再根据三角形中位线定理和直角三角形的性质求出DE和AE的长，进而由已知可判定四边形AEDF是平行四边形，从而求得其周长．

    解：在Rt△ABC中，∵AC=3，AB=4，
    ∴BC=5，
    ∵E是BC的中点，
    ∴AE=BE=2.5，
    ∴∠BAE=∠B，
    ∵∠FDA=∠B，
    ∴∠FDA=∠BAE，
    ∴DF∥AE，
    ∵D、E分别是AB、BC的中点，
    ∴DE∥AC，DE=AC=1.5，
    ∴四边形AEDF是平行四边形，
    ∴四边形AEDF的周长=2×（1.5+2.5）=8．
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

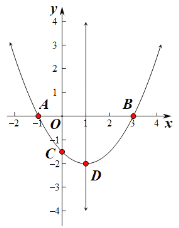
    【题目】抛物线交轴于点，，交轴的负半轴于，顶点为．下列结论：①；②；③当时，；④当是等腰直角三角形时，则；⑤若，是一元二次方程的两个根，且，则．其中错误的有（ ）个．

    A.5B.4C.3D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【题目】如图①，一次函数 y＝ x - 2 的图像交 x 轴于点 A，交 y 轴于点 B，二次函数 y＝ x2 bx c的图像经过 A、B 两点，与 x 轴交于另一点 C．

    （1）求二次函数的关系式及点 C 的坐标；

    （2）如图②，若点 P 是直线 AB 上方的抛物线上一点，过点 P 作 PD∥x 轴交 AB 于点 D，PE∥y 轴交 AB 于点 E，求 PD＋PE 的最大值；

    （3）如图③，若点 M 在抛物线的对称轴上，且∠AMB＝∠ACB，求出所有满足条件的点 M的坐标．

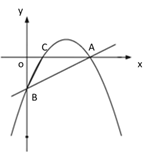
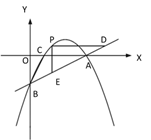
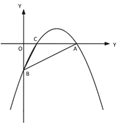
    ① ② ③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，AE是∠BAC的平分线，∠ABC的平分线 BM交AE于点M，点O在AB上，以点O为圆心，OB的长为半径的圆经过点M，交BC于点G，交 AB于点F．

    （1）求证：AE为⊙O的切线．

    （2）当BC=8，AC=12时，求⊙O的半径．

    （3）在（2）的条件下，求线段BG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

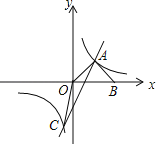
    【题目】如图，在平面直角坐标系中，直线y1＝2x﹣2与双曲线y2＝交于A、C两点，AB⊥OA交x轴于点B，且AB＝OA．

    （1）求双曲线的解析式；

    （2）连接OC，求△AOC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知矩形ABCD，AB=6，AD=10，请用直尺和圆规按下列步骤作图（不要求写作法，但要保留作图痕迹）；

    （1）在BC边上作出点E，使得cosBAE．

    （2）在（1）作出的图形中

    ①在CD上作出一点F，使得点D、E关于AF对称；

    ②四边形AEFD的面积=____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某乡镇在“精准扶贫”活动中销售农产品，经分析发现月销售量(万件与月份(月)的关系为: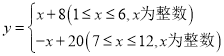

    每件产品的利润 (元)与月份(月)的关系如下表:

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    19

    18

    17

    16

    15

    14

    13

    12

    11

    10

    10

    10

    请你根据表格直接写出每件产品利润z (元) 与月份(月)的函数关系式;

    若月利润(万元) =当月销售量(万件) 当月每件产品的利润(元)，求月利润(万元)与月份(月)的关系式;

    当为何值时，月利润有最大值，最大值为多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．

    种类

    A

    B

    C

    D

    E

    出行方式

    共享单车

    步行

    公交车

    的士

    私家车

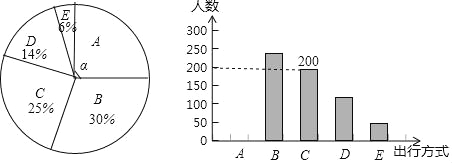
    根据以上信息，回答下列问题：

    （1）参与本次问卷调查的市民共有 人，其中选择B类的人数有 人；

    （2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；

    （3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A(﹣4，a)，B(﹣1，2)是一次函数y1=kx+b与反比例函数y2=(m＜0)图象的两个交点，AC⊥x轴于C．

    (1)求出k，b及m的值．

    (2)根据图象直接回答：在第二象限内，当y1＞y2时，x的取值范围是 ________．

    (3)若P是线段AB上的一点，连接PC，若△PCA的面积等于，求点P坐标．

    查看答案和解析>>

    同步练习册答案