
【题目】如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.

(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P坐标.
,求点P坐标.
【答案】(1) k=![]() ,b=
,b=![]() ,m=﹣2;(2) ﹣4<x<﹣1;(3) 点P的坐标为(﹣2,
,m=﹣2;(2) ﹣4<x<﹣1;(3) 点P的坐标为(﹣2,![]() )
)
【解析】
(1)把点B的坐标代入y=![]() 即可求出m的值,把点A的坐标代入反比例函数的解析式就可求出a,然后把A、B的坐标代入一次函数的解析式就可解决问题;
即可求出m的值,把点A的坐标代入反比例函数的解析式就可求出a,然后把A、B的坐标代入一次函数的解析式就可解决问题;
(2)运用数形结合的思想,结合图象即可解决问题;
(3)设点P的横坐标为xP,根据点A的坐标可得到AC的长,然后根据条件即可求出xP,然后将xP代入一次函数的解析式就可求出点P的坐标.
(1)把B(﹣1,2)代入y=![]() 得m=﹣1×2=﹣2,
得m=﹣1×2=﹣2,
把A(﹣4,a)代入y=﹣![]() 得a=﹣
得a=﹣![]() =
=![]() ,
,
把A(﹣4,![]() ),B(﹣1,2)代入y=kx+b,
),B(﹣1,2)代入y=kx+b,
得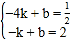 ,
,
解得:![]() ,
,
∴k=![]() ,b=
,b=![]() ,m=﹣2;
,m=﹣2;
(2)结合图象可得:在第二象限内,当y1>y2时,x的取值范围是﹣4<x<﹣1,
故答案为﹣4<x<﹣1;
(3)设点P的横坐标为xP,
∵AC⊥x轴,点A(﹣4,![]() ),
),
∴AC=![]() .
.
∵△PCA的面积等于![]() ,
,
∴![]() ×
×![]() ×[xP﹣(﹣4)]=
×[xP﹣(﹣4)]= ![]() ,
,
解得xP=﹣2,
∵P是线段AB上的一点,
∴yP=![]() ×(﹣2)+
×(﹣2)+![]() =
=![]() ,
,
∴点P的坐标为(﹣2,![]() ).
).


科目:初中数学 来源: 题型:
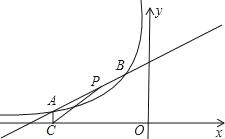
【题目】如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC交AC于点D,过点D作DE⊥AB交AB于点E,过C作CF∥BD交ED于F.
(1)求证:△BED≌△BCD;
(2)若∠A=36°,求∠CFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有2个空心菱形,第②个图形中一共有5个空心菱形,第③个图形中一共有11个空心菱形,…,按此规律排列下去,第⑨个图形中空心菱形的个数为( )

A.68B.76C.86D.104
查看答案和解析>>
科目:初中数学 来源: 题型:
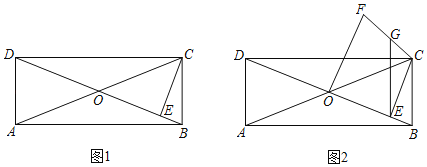
【题目】矩形ABCD的对角线相交于点O,∠COE=45°,过点C作CE⊥BD于点E,
(1)如图1,若CB=1,求△CED的面积;
(2)如图2,过点O作OF⊥DB于点O,OF=OD,连接FC,点G是FC中点,连接GE,求证:DC=2GE.
查看答案和解析>>
科目:初中数学 来源: 题型:
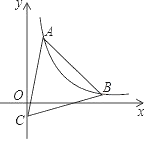
【题目】如图,△ABC是等边三角形,顶点C在y轴的负半轴上,点A(1,![]() ),点B在第一象限,经过点A的反比例函数y=
),点B在第一象限,经过点A的反比例函数y=![]() (x>0)的图象恰好经过顶点B,则△ABC的边长为_____.
(x>0)的图象恰好经过顶点B,则△ABC的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
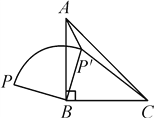
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )
A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先仔细阅读材料,再尝试解决问题:我们在求代数式![]() 的最大或最小值时,通过利用公式
的最大或最小值时,通过利用公式![]() 对式子作如下变形:
对式子作如下变形:
![]() ,
,
因为![]() ,
,
所以![]() ,
,
因此![]() 有最小值2,
有最小值2,
所以,当![]() 时,
时,![]() ,
,![]() 的最小值为2.
的最小值为2.
同理,可以求出![]() 的最大值为7.
的最大值为7.
通过上面阅读,解决下列问题:
(1)填空:代数式![]() 的最小值为______________;代数式
的最小值为______________;代数式![]() 的最大值为______________;
的最大值为______________;
(2)求代数式![]() 的最大或最小值,并写出对应的
的最大或最小值,并写出对应的![]() 的取值;
的取值;
(3)求代数式![]() 的最大或最小值,并写出对应的
的最大或最小值,并写出对应的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
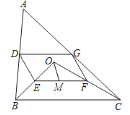
【题目】如图,点![]() 是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点
是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点![]() 、
、![]() 、
、![]() 、
、![]() 依次连结,得到四边形
依次连结,得到四边形![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 为
为![]() 的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com