
【题目】已知二次函数y=x2﹣2hx+h,当自变量x的取值在﹣1≤x≤1的范围中时,函数有最小值n,则n的最大值是_____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.

(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
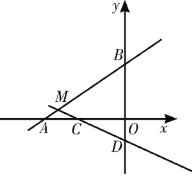
【题目】如图,在平面直角坐标系xOy中,已知直线AB:y=![]() x+4交x轴于点A,交y轴于点B.直线CD:y=-
x+4交x轴于点A,交y轴于点B.直线CD:y=-![]() x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标.
(2)若点P是射线MD的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系,并指出x的取值范围.
(3)当S=10时,平面直角坐标系内是否存在点E,使以点B,E,P,M为顶点的四边形是平行四边形?若存在,共有几个这样的点?请求出其中一个点的坐标(写出求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
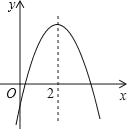
A. ac<0 B. ab>0 C. 4a+b=0 D. a﹣b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;
(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
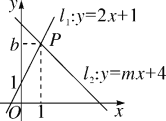
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线与直线l1,l2,分别交于点C,D,垂足为点E,设点E的坐标为(a,0)若线段CD长为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,![]() 校、
校、![]() 校各派出
校各派出![]() 名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
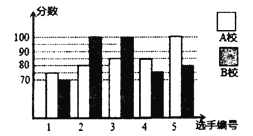
(1)根据图示填写下表:
平均数 | 中位数 | 众数 | |
|
| ||
|
| 80 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com