
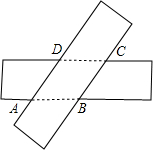
 把两张宽度相等的矩形纸片叠放在一起,得到如图的四边形ABCD.
把两张宽度相等的矩形纸片叠放在一起,得到如图的四边形ABCD.分析 1)由AD∥BC,DC∥AB,可得四边形ABCD是平行四边形.然后分别过点A、D作AE⊥BC于E,DF⊥AB于F.又由两张矩形纸片的宽度相等,即可得AE=DF,又由面积问题,可得BC=AB,即可得四边形ABCD为菱形;
(2)由题意可判断,当∠DAB=90°时,菱形ABCD为正方形,周长最小值为8.当AC为矩形纸片的对角线时,周长最大值为17.
解答 (1)证明:如图:分别过点A、D作AE⊥BC于E,DF⊥AB于F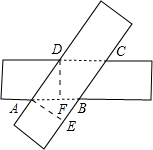 .
.
∵AD∥BC,DC∥AB,
∴四边形ABCD是平行四边形.
∵两张矩形纸片的宽度相等,
∴AE=DF,
又∵AE•BC=DF•AB=S?ABCD,
∴BC=AB,
∴?ABCD是菱形;
(2)解:存在最小值和最大值.
①当∠DAB=90°时,菱形ABCD为正方形,周长最小值为8;
②当AC为矩形纸片的对角线时,设AB=x.如图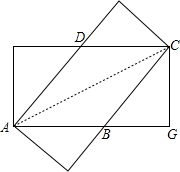 ,
,
在Rt△BCG中,BC2=CG2+BG2,
即x2=(8-x)2+22,x=$\frac{17}{4}$.
∴周长最大值为$\frac{17}{4}$×4=17.
点评 本题考查了菱形的判定,及运用矩形,菱形的性质进行综合运算的能力.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
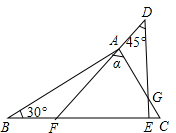 小雪是个爱动脑的同学,有一天她把手中的一副三角板拼在一起,如图所示,这样除了三角板原有的6个角外,又出现了几个角,如图图中的α,她想,能不能借助三角板中已知角的度数,把这些角分别求出来呢?经过一番思考,她发现图中其他8个角(包括∠α)的度数是可以求出来的!聪明的同学,请你把这些角找出来,然后一一求出它们的度数,相信你能行!
小雪是个爱动脑的同学,有一天她把手中的一副三角板拼在一起,如图所示,这样除了三角板原有的6个角外,又出现了几个角,如图图中的α,她想,能不能借助三角板中已知角的度数,把这些角分别求出来呢?经过一番思考,她发现图中其他8个角(包括∠α)的度数是可以求出来的!聪明的同学,请你把这些角找出来,然后一一求出它们的度数,相信你能行!查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
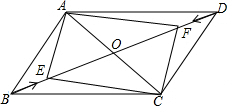 如图,在?ABCD中,对角线BD=8cm.AC=4cm.点E从点B出发沿BD方向以1cm/s的速度向点D运动,同时点F从点D出发沿着DB方向以同样的速度向点B运动,设点E,F运动的时间为t(s),其中0<t<8.
如图,在?ABCD中,对角线BD=8cm.AC=4cm.点E从点B出发沿BD方向以1cm/s的速度向点D运动,同时点F从点D出发沿着DB方向以同样的速度向点B运动,设点E,F运动的时间为t(s),其中0<t<8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com