

分析 根据BE=FD=$\frac{BD-EF}{2}$,即可求得BE的长,则BF即可求得,则在直角△ABF中,已知一个锐角和一直角边,利用正切函数即可求得AB的长.
解答 解:∵BE=FD=$\frac{BD-EF}{2}$=$\frac{444-36}{2}$=204米,
∴BF=BE+EF=204+36=240米,
∵在直角△ABF中,tan∠AFB=$\frac{AB}{BF}$,
∴AB=BF•tan∠AFB=240×tan28.2°≈240×0.536=129.6≈130米.
答:该桥的主塔AB高为130米
点评 本题考查了仰角的概念,以及解直角三角形的应用,难度一般,正确理解正切函数的定义,求得BF的长是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,且∠CDB=∠OBD=30°,⊙O的半径为6cm.
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,且∠CDB=∠OBD=30°,⊙O的半径为6cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
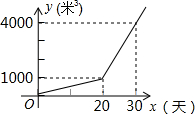 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示,当总用水量为2500米3时,该经济作物种植时间是25天.
某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示,当总用水量为2500米3时,该经济作物种植时间是25天.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com