
| k |
| x |
| 1 |
| 2 |
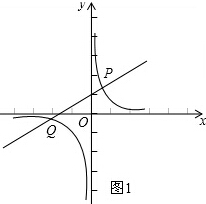 解:(1)如图1,
解:(1)如图1,| 1 |
| 2 |
| k |
| x |
|
|
| 2 |
| 3x |
| 2 |
| 3 |
|
|
|
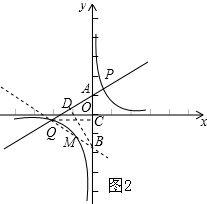
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
2
| ||
| 3 |
| QC |
| AC |
| 3 |
| 2 |
| QC |
| AC |
| 3 |
| 2 |
| DB |
| DA |
| 3 |
| 2 |
| DB |
| DQ |
| 3 |
| 3 |
| 3 |
2
| ||
| 3 |
2
| ||
3(
|
| 13 |
52-26
| ||
| 3 |
49-26
| ||
| 3 |
49-26
| ||
| 3 |
49-26
| ||
| 3 |
| 1 |
| 3 |
49-26
| ||
| 3 |
| 1 |
| 3 |
13
| ||
| 3 |
13
| ||
| 3 |
49-26
| ||
| 3 |
| 2 |
| 3x |
13
| ||
| 3 |
49-26
| ||
| 3 |
| 2 |
| 3x |
| 3 |
| 3 |
| 3 |
13
| ||
| 69 |
13
| ||
| 69 |
| 2 |
| 3x |
26
| ||
| 3 |
13
| ||
| 69 |
26
| ||
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
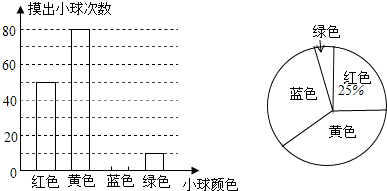
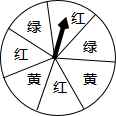 如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为
如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为查看答案和解析>>
科目:初中数学 来源: 题型:
| 学生 | 甲 | 乙 | 丙 | 丁 |
| 平均成绩 | 2.35 | 2.35 | 2.35 | 2.35 |
| 方差 | 0.35 | 0.25 | 0.2 | 0.3 |
| A、甲 | B、乙 | C、丙 | D、丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:
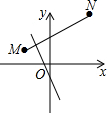 如图,在平面直角坐标系中,线段MN的端点坐标为M(-2,1),N(2,3),直线y=kx-1与线段MN有交点,则k的值不可能是( )
如图,在平面直角坐标系中,线段MN的端点坐标为M(-2,1),N(2,3),直线y=kx-1与线段MN有交点,则k的值不可能是( )| A、5 | ||
| B、-5 | ||
| C、2 | ||
D、-
|
查看答案和解析>>
科目:初中数学 来源: 题型:
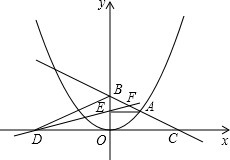 如图,在平面直角坐标系中,A是抛物线y=
如图,在平面直角坐标系中,A是抛物线y=| 1 |
| 2 |
| 2 |
| 3 |
| AF |
| BF |
| AF |
| BF |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在教学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
如图,在教学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com