
【题目】用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:

(1)a,b,c各表示几?
(2)这个几何体最少有几个小立方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体从左面看到的形状图.
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】某公司计划从本地向甲、乙两地运送海产品共30吨进行销售.本地与甲、乙两地都有铁路和公路相连(如图所示),铁路的单位运价为2元/(吨千米),公路的单位运价为3元/(吨千米).
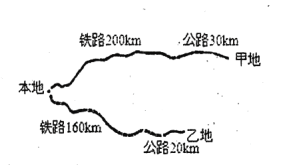
(1)公司计划从本地向甲地运输海产品![]() 吨,求总费用
吨,求总费用![]() (元)与
(元)与![]() 的函数关系式;
的函数关系式;
(2)公司要求运到甲地的海产品的重量不少于得到乙地的海产品重量的2倍,当![]() 为多少时,总运费
为多少时,总运费![]() 最低?最低总运费是多少元?(参考公式:货运运费
最低?最低总运费是多少元?(参考公式:货运运费![]() 单位运价
单位运价![]() 运输里程
运输里程![]() 货物重量)
货物重量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,顶点
,顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 的高
的高![]() 交线段
交线段![]() 于点
于点![]() ,且
,且![]() .
.
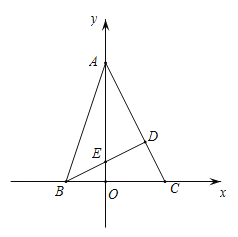
(1)求线段![]() 的长;
的长;
(2)动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以每秒
以每秒![]() 个单位长度的速度运动,
个单位长度的速度运动,![]() 、
、![]() 两点同时出发,且点
两点同时出发,且点![]() 到达
到达![]() 点处时
点处时![]() 、
、![]() 两点同时停止运动,设点
两点同时停止运动,设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,直接写出相应的
,直接写出相应的![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点![]() 是直线
是直线![]() 上的一点且
上的一点且![]() ,是否存在
,是否存在![]() 值,使以点
值,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与以点
为顶点的三角形与以点![]() 、
、![]() 、
、![]() 为顶点的三角形全等?若存在,请求出符合条件的
为顶点的三角形全等?若存在,请求出符合条件的![]() 值,若不存在,请说明理由.
值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )

A. 9 B. 10 C. 11 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,AB=3,BC=4.将△BCD沿对角线BD翻折得到△BED,BE交AD于点O.
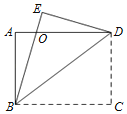
(1)判断△BOD的形状,并证明;(2)直接写出线段OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com