
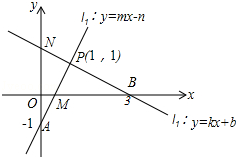
 如图,请根据图象所提供的信息解答下列问题:
如图,请根据图象所提供的信息解答下列问题:分析 (1)根据函数图象,当x≤1时,直线y=kx+b没有在直线y=mx+n的下方,即kx+b≥mx+n;
(2)观察函数图象,写出直线y=kx+b在x轴下方所对应的自变量的范围即可;
(3)利用函数图象交点坐标为两函数解析式组成的方程组的解进行解答;
(4)先利用待定系数法确定直线l1和l2的解析式,再根据坐标轴上点的坐标特征确定M点和N点坐标,然后利用四边形OMPN的面积=S△ONB-S△PMB进行计算.
解答 解:(1)当x≤1时,kx+b≥mx-n;
(2)不等式kx+b<0的解集为x>3;
(3)交点P的坐标(1,1)是二元一次方程组$\left\{\begin{array}{l}{y=mx-n}\\{y=kx+b}\end{array}\right.$的解;
(4)把A(0,-1),P(1,1)分别代入y=mx-n得$\left\{\begin{array}{l}{-n=-1}\\{m-n=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=2}\\{n=1}\end{array}\right.$,
所以直线l1的解析式为y=2x-1,
当y=0时,2x-1=0,解得x=$\frac{1}{2}$,
所以M点的坐标为($\frac{1}{2}$,0);
把P(1,1)、B(3,0)分别代入y=kx+b得$\left\{\begin{array}{l}{k+b=1}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
所以直线l2的解析式为y=-$\frac{1}{2}$x+$\frac{3}{2}$,
当x=0时,y=-$\frac{1}{2}$x+$\frac{3}{2}$=$\frac{3}{2}$,则N点坐标为(0,$\frac{3}{2}$),
所以四边形OMPN的面积=S△ONB-S△PMB
=$\frac{1}{2}$×3×$\frac{3}{2}$-$\frac{1}{2}$×(3-$\frac{1}{2}$)×1
=1.
点评 本题考查了一次函数与二元一次方程组、与一元一次不等式的关系,函数图象交点坐标为两函数解析式组成的方程组的解.也考查了待定系数法求一次函数解析式.


科目:初中数学 来源: 题型:选择题
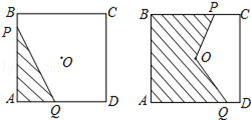 如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为y cm2,那么y与x的函数关系图象可能是( )
如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为y cm2,那么y与x的函数关系图象可能是( )| A. | 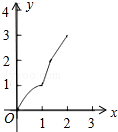 | B. | 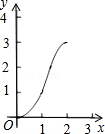 | C. | 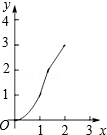 | D. | 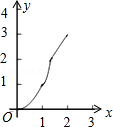 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
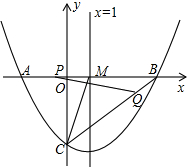 如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com