
【题目】如图,AB是⊙O的直径,C、D为⊙O上两点,且![]() ,过点O作OE⊥AC于点E,⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
,过点O作OE⊥AC于点E,⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
(1)求证:∠F=∠B;
(2)若AB=10,BG=13,求AF的长.
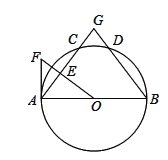
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据圆周角定理得到∠GAB=∠B,根据切线的性质得到∠GAB+∠GAF=90°,证明∠F=∠GAB,等量代换即可证明;
(2)连接OG,根据勾股定理求出OG,证明△FAO∽△BOG,根据相似三角形的性质列出比例式,计算即可.
(1)∵![]() ,
,
∴![]() ,
,
∴∠GAB=∠B,
∵AF是⊙O的切线,
∴AF⊥AO,
∴∠GAB+∠GAF=90°,
∵OE⊥AC,
∴∠F+∠GAF=90°,
∴∠F=∠GAB,
∴∠F=∠B;
(2)连接OG,
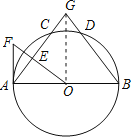
∵∠GAB=∠B,
∴AG=BG,
∵OA=OB=5,
∴OG⊥AB,
∴OG=![]() =
=![]() =8,
=8,
∵∠FAO=∠BOG=90°,∠F=∠B,
∴△FAO∽△BOG,
∴![]() ,
,
∴AF=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识重现)我们知道,在ax=N中,已知底数a,指数x,求幂N的运算叫做乘方运算.例如23=8;已知幂N,指数x,求底数a的运算叫做开方运算,例如![]() =2;
=2;
(学习新知)
现定义:如果ax=N(a>0且a≠1),即a的x次方等于N(a>0且a≠1),那么数x叫做以a为底N的对数(logarithm),记作x=logaN.其中a叫做对数的底数,N叫做真数,x叫做以a为底N的对数.例如log28=3.零没有对数;在实数范围内,负数没有对数.
(应用新知)
(1)填空:在ax=N,已知幂N,底数a(a>0且a≠1),求指数x的运算叫做_____运算;
(2)选择题:在式子log5125中,真数是_____
A.3 B.5 C.10 D.125
(3)①计算以下各对数的值:log39;log327;log3243.
②根据①中计算结果,请你直接写出logaM,logaN,loga(MN)之间的关系.(其中a>0且a≠1,M>0,N>0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动.
上运动.
(1)求直线![]() 的解析式.
的解析式.
(2)求![]() 的面积.
的面积.
(3)是否存在点![]() ,使
,使![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ?若存在求出此时点
?若存在求出此时点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
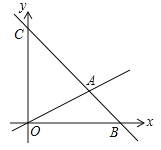
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①GP=GD;②∠BAD=∠ABC;③点P是△ACQ的外心;④![]() .其中正确的是______________(填序号)
.其中正确的是______________(填序号)
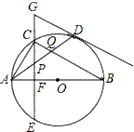
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC=3![]() ,求DE的长;
,求DE的长;
(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3![]() ,求图中阴影部分面积.
,求图中阴影部分面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
(1)容器内原有水多少?
(2)求W与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?

图 ① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
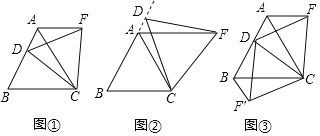
【题目】综合与探究
(1)操作发现:如图1,点D是等边△ABC边BA上一动点(点D与点B不重合),连结DC,以DC为边在CD上方作等边△DCF,连结AF,你能发现线段AF与BD之间的数量关系吗?证明你发现的结论.
(2)类比猜想:如图2,当动点D运动至等边△ABC边BA的延长线上时,其余条件不变,猜想:(1)中的结论是否成立,并说明理由.
(3)拓展探究:如图3.当动点D在等边△ABC边BA上运动时(点D与点B不重合),连结DC,以DC为边在CD上方和下方分别作等边△DCF和等边△DCF′,连结AF,BF′,探究:AF、BF′与AB有何数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com