
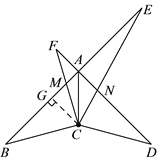
【题目】如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)先证明△ABC≌△ADC,然后再证明△ACF≌△ACE即可得;
(2)过点C作CG⊥AB于点G,先求出AC的长,再证明△ACF∽△AEC,根据相似三角形的性质即可得.
试题解析:(1)∵AB=AD,BC=CD,AC=AC,∴△ABC≌△ADC,
∴∠BAC=∠DAC=45°,∴180°-∠BAC=180°-∠DAC,∴∠FAC=∠EAC=135°,
又∵∠FCA=∠ECA,
∴△ACF≌△ACE,
∴AE=AF;
(2)过点C作CG⊥AB于点G,则∠BGC=∠AGC=90°,
∵∠B=30°,∴CG=![]() BC=
BC=![]() =1,
=1,
∵∠BAC=45°,∴AC=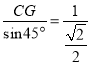 =
=![]() ,
,
∵∠FAC=∠EAC=135°,∴∠ACF+∠F=45°,
又∵∠ACF+∠ACE=45°,∴∠F=∠ACE,
∴△ACF∽△AEC,
∴![]() ,即
,即![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
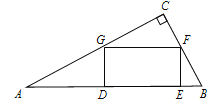
【题目】如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上.
(1)求证:△ADG∽△FEB;
(2)若AG=5,AD=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
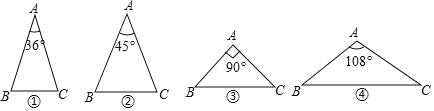
A. ①③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共180件其进价和售价如表:(注:获利=售价进价)
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,BC=6cm,射线AG//BC,点E从点A出发,沿射线AG以1cm/s的速度运动,同时点F从点B出发,沿射线BC以2cm/s的速度运动,设运动时间为t,当t为( )s时,以A,F,C,E为顶点的四边形是平行四边形?( )

A.2B.3C.6D.2或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上运动(不与点
上运动(不与点![]() 重合).
重合).
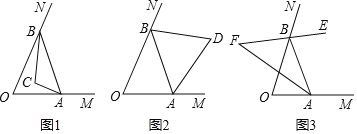
(1)如图1,若![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,若![]() ,
,![]() 的外角
的外角![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,则
,则![]() 等于______度(用含字母
等于______度(用含字母![]() 的代数式表示);
的代数式表示);
(3)如图3,若![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 的反向延长线与
的反向延长线与![]() 的平分线交于点
的平分线交于点![]() .试问:随着点
.试问:随着点![]() 、
、![]() 的运动,
的运动,![]() 的大小会变吗?如果不会,求
的大小会变吗?如果不会,求![]() 的度数;如果会,请说明理由.
的度数;如果会,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 的“
的“![]() 值”定义如下:若点
值”定义如下:若点![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 长度的最大值与最小值之差即为点
长度的最大值与最小值之差即为点![]() 的“
的“![]() 值”,记为
值”,记为![]() .特别的,当点
.特别的,当点![]() ,
, ![]() 重合时,线段
重合时,线段![]() 的长度为0.
的长度为0.
当⊙![]() 的半径为2时:
的半径为2时:
(1)若点![]() ,
, ![]() ,则
,则![]() _________,
_________, ![]() _________;
_________;
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求出点
,求出点![]() 的横坐标;
的横坐标;
(3)直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点
轴分别交于点![]() ,
, ![]() .若线段
.若线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,请你直接写出
,请你直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用6000元购进A、B两款新式服装,按标价出售后可获毛利润3800元(利润=售价-进价),这两款服装的进价、标价如下表所示:
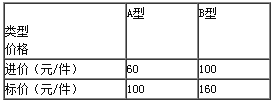
(1)求这两种服装各购进的件数;
(2)由于市场竞争激烈,A款服装只能按标价的9折出售,B款服装只能按标价的8折出售,那么这批服装全部售完后,服装店毛利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com