
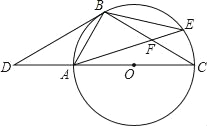
【题目】如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
(1)证明:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为16,cos∠BFA=![]() ,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
【答案】(1)证明见解析;(2)36.
【解析】(1)BD是⊙O的切线.先连接OB,由于AC是直径,那么∠ABC=90°,于是∠1+∠C=90°,而OA=OB,可得∠1=∠2,结合∠3=∠C,易得∠2+∠3=90°,从而可证DB是⊙O的切线;
(2)由于cos∠BFA=![]() ,那么
,那么![]() ,利用圆周角定理可知∠E=∠C,∠4=∠5,易证△EBF∽△CAF,于是
,利用圆周角定理可知∠E=∠C,∠4=∠5,易证△EBF∽△CAF,于是![]() ,从而易求△ACF的面积.
,从而易求△ACF的面积.
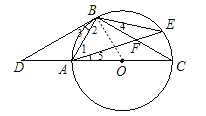
(1)BD是⊙O的切线.理由如下:
如图所示,连接OB.
∵AC是⊙O的直径,∴∠ABC=90°,∴∠1+∠C=90°.
∵OA=OB,∴∠1=∠2,∴∠2+∠C=90°.
∵∠3=∠C,∴∠2+∠3=90°,∴DB是⊙O的切线;
(2)在Rt△ABF中.
∵cos∠BFA=![]() .
.
∵∠E=∠C,∠4=∠5,∴△EBF∽△CAF,
∴![]() ,即
,即![]() ,解得:S△ACF=22.5.
,解得:S△ACF=22.5.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
材料一:
自然数的发现是人类数学研究的开端,我们在研究自然数的时候采用的进制为十进制.现定义:位数相同且对应数位上的数字之和为10的两个数互为“亲密数”,例如:3与7互为“亲密数”,16的“亲密数”为94.
材料二:
若![]() 的“亲密数”为
的“亲密数”为![]() ,记
,记![]() 为
为![]() 的“亲密差”例如:72的“亲密数”为38.
的“亲密差”例如:72的“亲密数”为38.
![]() ,则34为72的“亲密差”.
,则34为72的“亲密差”.
根据材料,回答下列问题:
(1)请填空:64的“亲密数”为______;25的“亲密差”为______;
(2)某两位数个位上的数字比十位上的数字大2,且这个两位数的“亲密数”等于它的![]() 倍,求这个两位数的“亲密差”:
倍,求这个两位数的“亲密差”:
(3)某个三位数![]() (
(![]() ,且
,且![]() 为整数),记
为整数),记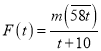 ,若
,若![]() 的值为一个整数,求这个整数
的值为一个整数,求这个整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
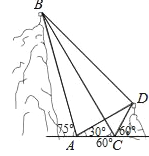
【题目】如图,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°.于水面C处测得B点和D点的仰角均为60°,AC=0.1km.
(1)试探究图中B,D间距离与另外哪两点间距离相等;
(2)求B点距水平面的高度(计算结果精确到0.01km,参考数据:![]() ≈1.73,tan75°≈3.73)
≈1.73,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
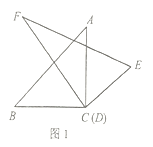
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
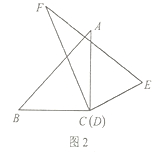
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
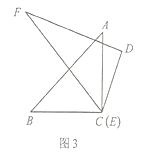
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
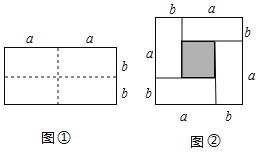
【题目】(1)如图①是一个长为2a,宽为2b的长方形,若将此图中虚线用剪刀均分为四块小长方形,然后按图②的形状拼成一个正方形,请问:这两个图形的什么量不变?请填写这个量的名称 .所得的正方形的面积比原长方形的面积多出的阴影部分的面积用含a,b的代数式表示 ;
(2)由①的探索中,可以得出的结论是:在周长一定的长方形中,当 时,面积最大;
(3)若一长方形的周长为36厘米,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,則四辺形ABFD的周长为( )

A. 16cmB. 18cmC. 20cmD. 22cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.若∠AOD=120°,AC=4,则CD的大小为( )
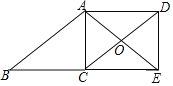
A.8B.4![]() C.8
C.8![]() D.6
D.6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知三点A、B、C.
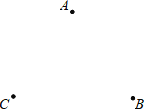
(1)请读下列语句,并分别画出图形
画直线AB;画射线AC;连接BC.
(2)在(1)的条件下,图中共有 条射线.
(3)从点C到点B的最短路径是 ,依据是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com