
分析 (1)在前面乘一个(2-1),然后再连续利用平方差公式计算;
(2)在前面乘一个2×(1-$\frac{1}{2}$),然后再连续利用平方差公式计算;
(3)把每个因式逆用平方差公式分解,然后根据乘法结合率和有理数的乘法计算即可.
解答 解:(1)(2+1)(22+1)(24+1)(28+1)…(22004+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)…(22004+1)
=(22-1)(22+1)(24+1)(28+1)…(22004+1)
=(24-1)(24+1)(28+1)…(22004+1)
=24008-1;
(2)$(1+\frac{1}{2})(1+\frac{1}{2^2})(1+\frac{1}{2^4})(1+\frac{1}{2^8})+\frac{1}{{{2^{15}}}}$
=2×(1-$\frac{1}{2}$)$(1+\frac{1}{2})(1+\frac{1}{2^2})(1+\frac{1}{2^4})(1+\frac{1}{2^8})+\frac{1}{{{2^{15}}}}$
=2×(1-$\frac{1}{{2}^{16}}$)+$\frac{1}{{2}^{15}}$
=2-$\frac{1}{{2}^{15}}$+$\frac{1}{{2}^{15}}$
=2;
(3)$(1-\frac{1}{2^2})(1-\frac{1}{3^2})(1-\frac{1}{4^2})…(1-\frac{1}{{{{100}^2}}})$
=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)…(1-$\frac{1}{100}$)(1+$\frac{1}{100}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×…×$\frac{99}{100}$×$\frac{101}{100}$
=$\frac{1}{2}$×$\frac{101}{100}$,
=$\frac{101}{200}$.
点评 本题考查了平方差公式的运用,熟练掌握平方差公式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
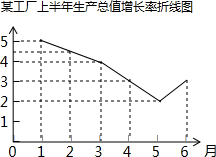 某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )
某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )| A. | 1~5月份生产总值增长率逐月减少 | |
| B. | 6月份生产总值的年增长率开始回升 | |
| C. | 这半年中每月的生产总值不断增长 | |
| D. | 这半年中每月的生产总值有增有减 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com