
 某批足球的质量检测结果如下:
某批足球的质量检测结果如下:| 抽取足球数n | 100 | 200 | 400 | 600 | 800 | 1000 |
| 合格的频数m | 93 | 192 | 384 | 564 | 759 | 950 |
| 合格的频率$\frac{m}{n}$ | 0.93 | 0.96 | 0.96 | 0.94 | 0.95 | 0.95 |
分析 (1)根据频率=频数÷总数计算可得;
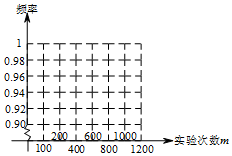
(2)由表格中数据在坐标系内用点描出来,再用线段依次相连即可得;
(3)根据频率估计概率,频率都在0.95左右波动,所以任意抽取的一只足球是合格品的概率估计值是0.95.
解答 解:(1)完成表格如下:
| 抽取足球数n | 100 | 200 | 400 | 600 | 800 | 1000 |
| 合格的频数m | 93 | 192 | 384 | 564 | 759 | 950 |
| 合格的频率$\frac{m}{n}$ | 0.93 | 0.96 | 0.96 | 0.94 | 0.95 | 0.95 |
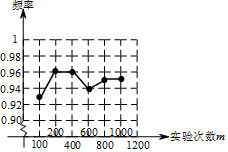
点评 本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.也考查了频率分布折线图.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
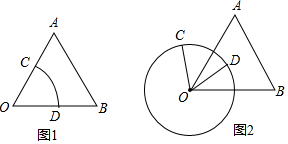
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
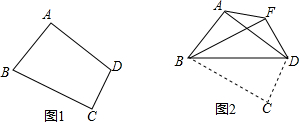
 如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是①.(填番号)
如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是①.(填番号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
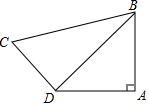 如图:四边形ABCD中,AB=4,BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,AD=4,∠A=90°,求∠ADC的度数.
如图:四边形ABCD中,AB=4,BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,AD=4,∠A=90°,求∠ADC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com