
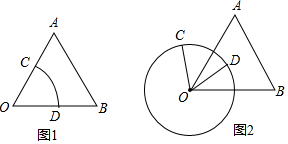
分析 (1)直接利用旋转的性质结合平行线的性质得出旋转角;
(2)利用旋转的性质结合全等三角形的判定与性质得出答案.
解答 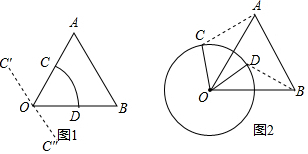 解:(1)如图1所示:
解:(1)如图1所示:
当OC′∥AB时,此时∠A=∠AOC′=60°,即旋转角α为60°,
当OC″∥AB时,此时∠B=∠BOC′=60°,即旋转角α为:60°+180°=240°;
综上所述:α为60或240度;
故答案为:60或240;
(2)AC=BD,
理由:如图2所示:由题意可得,CO=DO,AO=BO,∠COA=∠BOD,
在△COA和△DOB中
$\left\{\begin{array}{l}{CO=DO}\\{∠COA=∠BOD}\\{OA=OB}\end{array}\right.$,
则△COA≌△DOB(SAS),
故AC=BD.
点评 此题主要考查了旋转的性质以及等边三角形的性质、全等三角形的判定与性质等知识,正确把握相关性质是解题关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
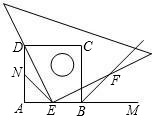 如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.
如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
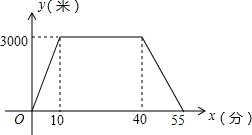 娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )
娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )| A. | 娟娟同学与超市相距3000m | |
| B. | 娟娟同学去超市途中的速度是300m/min | |
| C. | 娟娟同学在超市逗留了30min | |
| D. | 娟娟同学从超市返回家比从家里去超市的速度快 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
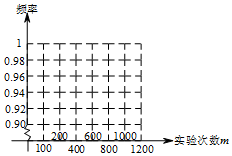 某批足球的质量检测结果如下:
某批足球的质量检测结果如下:| 抽取足球数n | 100 | 200 | 400 | 600 | 800 | 1000 |
| 合格的频数m | 93 | 192 | 384 | 564 | 759 | 950 |
| 合格的频率$\frac{m}{n}$ | 0.93 | 0.96 | 0.96 | 0.94 | 0.95 | 0.95 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )| A. | ∠BAC与∠B是同旁内角 | B. | AB与AC互相垂直 | ||
| C. | 点A与直线BC的垂线段为线段AD | D. | 点A到BC的距离是线段AD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间的连线中,直线最短 | |
| B. | 若AP=BP,则P是线段AB的中点 | |
| C. | 若P是线段AB的中点,则AP=BP | |
| D. | 两点之间的线段叫做这两点之间的距离 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com