[题目]按要求完成下列证明如图.AB∥CD.CB∥DE.求证:∠B+∠D=180°．证明:∵AB∥CD.∴∠B=()．∵CB∥DE.∴∠C+=180°()．∴∠B+∠D=180°．题目和参考答案——青夏教育精英家教网—

【题目】按要求完成下列证明
如图，AB∥CD，CB∥DE，求证：∠B+∠D=180°．
证明：∵AB∥CD，
∴∠B=（）．
∵CB∥DE，
∴∠C+=180°（）．
∴∠B+∠D=180°．

【答案】∠C；两直线平行，内错角相等；∠D；两直线平行，同旁内角互补
【解析】证明：∵AB∥CD，
∴∠B=∠C （两直线平行，内错角相等），
∵CB∥DE，
∴∠C+∠D=180°（两直线平行，同旁内角互补），
∴∠B+∠D=180°．
所以答案是：∠C，两直线平行，内错角相等；∠D；两直线平行，同旁内角互补．
【考点精析】利用平行线的性质对题目进行判断即可得到答案，需要熟知两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】据调查，2013年5月济南市的房价均价为7600元/m2，2015年同期达到8200元/m2，假设这两年济南市房价的平均增长率为x，根据题意，所列方程为（　　）

A. 7600（1+x%）2＝8200B. 7600（1﹣x%）2＝8200

C. 7600（1+x）2＝8200D. 7600（1﹣x）2＝8200

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】不等式x﹣2≤0的解集是（　　）

A. x＞2 B. x＜2 C. x≥2 D. x≤2

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】根据等式和不等式的性质，可以得到：若a﹣b＞0，则a＞b；若a﹣b=0，则a=b；若a﹣b＜0，则a＜b．这是利用“作差法”比较两个数或两个代数式值的大小．
（1）试比较代数式5m2﹣4m+2与4m2﹣4m﹣7的值之间的大小关系；
解：（5m2﹣4m+2）﹣（4m2﹣4m﹣7）=5m2﹣4m+2﹣4m2+4m+7=m2+9，因为m2≥0
所以m2+9＞0
所以5m2﹣4m+24m2﹣4m﹣7．（用“＞”或“＜”填空）
（2）已知A=5m2﹣4（ m﹣ ），B=7（m2﹣m）+3，请你运用前面介绍的方法比较代数式A与B的大小．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知△ABC中，∠A=30°．
（1）如图①，∠ABC、∠ACB的角平分线交于点O，则∠BOC=°．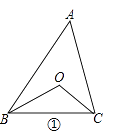
（2）如图②，∠ABC、∠ACB的三等分线分别对应交于O1、O2 ，则∠BO2C=°．
（3）如图③，∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1（内部有n﹣1个点），求∠BOn﹣1C（用n的代数式表示）．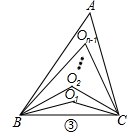
（4）如图③，已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1 ，若∠BOn﹣1C=60°，求n的值．