
【题目】如图,AB∥CD,E为AB上一点,∠BED=2∠BAD. 
(1)求证:AD平分∠CDE;
(2)若AC⊥AD,∠ACD+∠AED=165°,求∠ACD的度数.
【答案】
(1)证明:∵AB∥CD,
∴∠BED=∠EDC,∠BAD=∠ADC,
又∠BED=2∠BAD,
∴∠EDC=2∠ADC,
∴AD平分∠CDE
(2)解:依题意设∠ADC=∠ADE=∠BAD=x,
∴∠BED=∠EDC=2x,∠AED=180°﹣2x,
∵AB∥CD,
∴∠BAC+∠ACD=180°,即∠ACD=90°﹣x,
又∵∠ACD+∠AED=165°,
即90°﹣x+180°﹣2X=165°,
∴x=35°,
∴∠ACD=90°﹣x=90°﹣35°=55°
【解析】(1)根据平行线的性质得到∠BED=∠EDC,∠BAD=∠ADC,等量代换得到∠EDC=2∠ADC,由角平分线的定义即可得到结论;(2)设∠ADC=∠ADE=∠BAD=x,于是得到∠BED=∠EDC=2x,∠AED=180°﹣2x,根据平行线的性质得到∠BAC+∠ACD=180°,于是列方程90°﹣x+180°﹣2X=165°,即可得到结论.


科目:初中数学 来源: 题型:
【题目】按要求完成下列证明
如图,AB∥CD,CB∥DE,求证:∠B+∠D=180°.
证明:∵AB∥CD,
∴∠B=().
∵CB∥DE,
∴∠C+=180°().
∴∠B+∠D=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE为△ABC的边BC的垂直平分线,交BC于E,交AB于D,且∠B=40°,∠A=60°,则∠ACD的度数为( ) 
A.40°
B.50°
C.30°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,l与m相交于P点.若∠BAC=60°,∠ACP=24°,则∠ABP是( ) 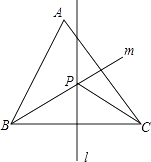
A.24°
B.30°
C.32°
D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校冬季运动会上,有15名选手参加了200米预赛,取前八名进入决赛.已知参赛选手成绩各不相同,某选手要想知道自己是否进入决赛,除了知道自己的成绩外,还需要了解全部成绩的( )
A. 平均数 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四舍五入法按要求对3.1415926分别取近似值,其中错误的是( )
A. 3.1(精确到0.1) B. 3.141(精确到千分位)
C. 3.14(精确到百分位) D. 3.1416(精确到0.0001)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com