
【题目】如图,锐角三角形ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,l与m相交于P点.若∠BAC=60°,∠ACP=24°,则∠ABP是( ) 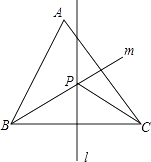
A.24°
B.30°
C.32°
D.36°
【答案】C
【解析】解:∵BP平分∠ABC, ∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠CBP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
解得:∠ABP=32°.
故选:C.
【考点精析】关于本题考查的三角形的内角和外角和线段垂直平分线的性质,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680,试根据以上数据求出潜艇C离开海平面的下潜深度。(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5. ![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=30°.
(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC=°. 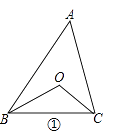
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2 , 则∠BO2C=°. 
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示). 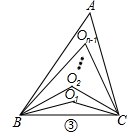
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1 , 若∠BOn﹣1C=60°,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”贯穿欧亚大陆,东边连接亚太经济圈,西边进入欧洲经济圈,大致涉及65个国家,总人口44亿,生产总值23万亿美元.将23万用科学记数法表示应为( )
A. 23×104B. 2.3×105C. 2.3×104D. 0.23×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,E为AB上一点,∠BED=2∠BAD. 
(1)求证:AD平分∠CDE;
(2)若AC⊥AD,∠ACD+∠AED=165°,求∠ACD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
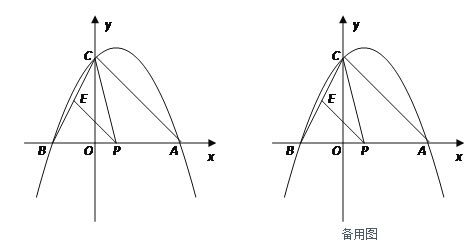
【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明“三角形的外角和等于360°”. 如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.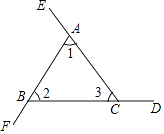
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com