
【题目】如图,在平面直角坐标系中,直线y=0.5x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,过点D作DE⊥x轴,垂足为E.
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.

【答案】(1)、A(-4,0) B(0,2) AB=2![]() ;(2)、(-6,4);(3)、M(-2,0)
;(2)、(-6,4);(3)、M(-2,0)
【解析】
试题分析:(1)、分别令x=0和y=0,求出点B和点A的坐标;(2)、利用△ADE和△AOB全等得出点D的坐标;(3)、作点B关于x轴的对称点F,连接DF与x轴的交点就是点M.
试题解析:(1)、当x=0时,y=2;当y=0时,x=-4 ∴A(-4,0) B(0,2)
∴OA=4 OB=2 ∴AB=![]()
(2)、∵ABCD为正方形 ∴AB=AD ∠DAB=90° ∵∠DEA=90°
∴∠EDA+∠DAE=90° ∠DAE+∠BAO=90° ∴∠EDA=∠BAO 又∵∠DEA=∠AOB=90°
∴△ADE≌△BAO ∴DE=A0=4 AE=OB=2 ∴OE=AO+AE=6 ∴点D的坐标为(-6,4)
(3)、作点B关于x轴的对称点F,则点F的坐标为(0,-2)
∴经过点DF的直线解析式为:y=-x-2 当y=0时,x=-2
即点M的坐标为:(-2,0).


科目:初中数学 来源: 题型:
【题目】武汉开发区一初中官士墩校区前期建设投入约153000000元.数据153000000用科学记数法可表示为_________________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D落到D’处,折痕为EF.
(1)、求证:△ABE≌△AD’F;
(2)、连接CF,判断四边形AECF是否为平行四边形?请证明你的结论。
(3)、若AE=5,求四边形AECF的周长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店出售甲、乙、丙三种不同型号的电动车,已知甲型车的第一季度销售额占这三种车总销售额的56%,第二季度乙、丙两种型号车的销售额比第一季度减少了a%,但该商场电动车的总销售额比第一季度增加了12%,且甲型车的销售额比第一季度增加了23%,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
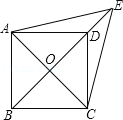
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2


(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+b)、(a+2b),不画图形,试通过计算说明需要C类卡片多少张;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积等于a2+5ab+4b2,画出这个长方形,并根据图形对多项式a2+5ab+4b2进行因式分解;
(3) 如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案并判断,将正确关系式的序号填写在横线上______ _____(填写序号)
①.xy =![]() ②.x+y=m ③.x2-y2=m·n ④.x2+y2 =
②.x+y=m ③.x2-y2=m·n ④.x2+y2 =![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com