
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA����4��3����B����3��1����C����1��3����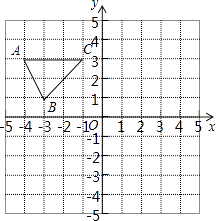
��1���밴����Ҫ��ͼ��
�ٽ���ABC������ƽ��4����λ���ȡ�������ƽ��2����λ���ȣ��õ���A1B1C1 �� ������A1B1C1��
�ڡ�A2B2C2���ABC����ԭ��O�����ĶԳƣ�������A2B2C2 ��
��2���ڣ�1�������õġ�A1B1C1�͡�A2B2C2���ڵ�M�����ĶԳƣ���ֱ��д���Գ�����M������꣮
 ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڹ���x�ķ�ʽ���� ![]() �ٺ�һԪ���η��̣�2��k��x2+3mx+��3��k��n=0���У�k��m��n��Ϊʵ�������̢ٵĸ�Ϊ�Ǹ�����
�ٺ�һԪ���η��̣�2��k��x2+3mx+��3��k��n=0���У�k��m��n��Ϊʵ�������̢ٵĸ�Ϊ�Ǹ�����
��1����k��ȡֵ��Χ��
��2�������̢�������������x1��x2 �� kΪ��������k=m+2��n=1ʱ���̢ڵ���������
��3�������̢�������ʵ����x1��x2 �� ����x1��x1��k��+x2��x2��k��=��x1��k����x2��k������kΪ������ʱ�����ж�|m|��2�Ƿ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��x2+2x����ԭ��O������ֱ��y=x��2����B��C���㣮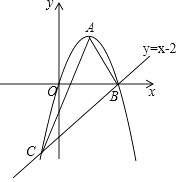
��1���������ߵĶ���A�����꼰��B��C�����ꣻ
��2����֤����ABC=90�㣻
��3����ֱ��BC�Ϸ������������Ƿ���ڵ�P��ʹ��PBC�������������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��4������NΪx���ϵ�һ�����㣬����N��MN��x���������߽��ڵ�M�����Ƿ������O��M��NΪ��������������ABC���ƣ������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ����x�ύ�ڵ�A���뷴��������y= ![]() ��x��0����ͼ���ڵ�B��2��n��������B��BC��x���ڵ�C����P��3n��4��1���Ǹ÷���������ͼ���ϵ�һ�㣬�ҡ�PBC=��ABC������������һ�κ����ı���ʽ��
��x��0����ͼ���ڵ�B��2��n��������B��BC��x���ڵ�C����P��3n��4��1���Ǹ÷���������ͼ���ϵ�һ�㣬�ҡ�PBC=��ABC������������һ�κ����ı���ʽ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������棺��¿��װ50����ÿ���ۼ�300Ԫ����һ���Թ�����10��ʱ���ۼ۲��䣻��һ���Թ���10��ʱ��ÿ����1���������ÿ����װ���ۼ۾�����2Ԫ����֪�÷�װ�ɱ���ÿ��200Ԫ����˿�һ���Թ����װx��ʱ����������л���yԪ��
��1����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���˿�һ���Թ�����ټ�ʱ����������л�����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���O�ǡ�ABC�����ģ�����OB��OC������O��EF��BC�ֱ�AB��AC�ڵ�E��F����֪BC=a ��a�dz����������ABC���ܳ�Ϊy����AEF���ܳ�Ϊx��������ͼ���У����±�ʾy��x֮��ĺ�����ϵ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿѧ�����������ʣ������������Ź涨ѧ��ÿ��μӻ�����ƽ��ʱ�䲻����1Сʱ��Ϊ�˽�ѧ���μӻ�����������Բ���ѧ���μӻ�����ʱ����г������飬����������������������������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺ 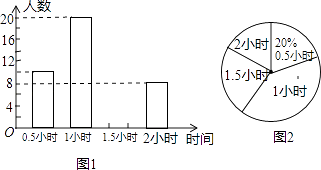
��1��һ�������˶�����ѧ����
��2���벹ȫ����ͳ��ͼ��
��3������У����6000��ѧ�����������ϵ��������Ƹ�Уȫ��ѧ��ÿ����뻧�����õ���ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ�Ըж�����Ϊ�������������ٰ����ĸ���Ŀ�ı��������Ƿֱ����ݽ������衢�鷨���滭��Ҫ��ÿλͬѧ����μӣ����ޱ�һ�����Ծ��꼶��1����Ϊ��������ͳ�ƣ�����ͳ�ƽ�������ͼ1��ͼ2��ʾ������ͳ��ͼ��������ͼʾ����������Ϣ����������⣮ 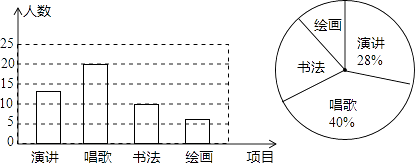
��1������μӻ滭������ѧ������ռȫ���������İٷֱȣ�
��2���������ͳ��ͼ�вμ��鷨������ѧ����������Բ�ĽǵĶ�����
��3������У���꼶ѧ����600�ˣ�����������������У��μ��ݽ��ͳ����ѧ�����ж����ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com