
【题目】问题情境:
平面直角坐标系中,矩形纸片OBCD按如图的方式放置![]() 已知
已知![]() ,
,![]() ,将这张纸片沿过点B的直
,将这张纸片沿过点B的直
线折叠,使点O落在边CD上,记作点A,折痕与边OD交于点E.
数学探究:
![]() 点C的坐标为______;
点C的坐标为______;
![]() 求点E的坐标及直线BE的函数关系式;
求点E的坐标及直线BE的函数关系式;
![]() 若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?
若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?
若存在,直接写出相应的点Q的坐标;若不存在,说明理由.

【答案】(1)(10,6);(2)![]() ),
),![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)根据矩形性质可得到C的坐标;(2)设![]() ,由折叠知,
,由折叠知,![]() ,
,![]() ,在
,在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,![]() ,在
,在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,即
,即![]() ,解得
,解得![]() ,可得
,可得![]() ;由待定系数法可求直线BE的解析式;(3)存在,理由:由
;由待定系数法可求直线BE的解析式;(3)存在,理由:由![]() 知,
知,![]() ,
,![]() ,设
,设![]() ,分两种情况分析:
,分两种情况分析:![]() 当BQ为的对角线时;
当BQ为的对角线时;![]() 当BQ为边时.
当BQ为边时.
解:![]() 四边形OBCD是矩形,
四边形OBCD是矩形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故答案为:![]() ;
;![]() 四边形OBCD是矩形,
四边形OBCD是矩形,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
由折叠知,![]() ,
,![]() ,
,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,![]() ,
,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设直线BE的函数关系式为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 直线BE的函数关系式为
直线BE的函数关系式为![]() ;
;![]() 存在,理由:由
存在,理由:由![]() 知,
知,![]() ,
,![]() ,
,![]() 能使以A,B,P,Q为顶点的四边形是平行四边形,
能使以A,B,P,Q为顶点的四边形是平行四边形,![]() ,
,![]() 当BQ为的对角线时,
当BQ为的对角线时,![]() ,
,![]() 点B,P在x轴,
点B,P在x轴,![]() 的纵坐标等于点A的纵坐标6,
的纵坐标等于点A的纵坐标6,![]() 点Q在直线BE:
点Q在直线BE:![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 当BQ为边时,
当BQ为边时,![]() 与BP互相平分,
与BP互相平分,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
即:直线BE上是存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形,点![]() 或
或![]() .
.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( ) 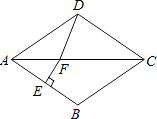
A.55°
B.65°
C.75°
D.85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A∶∠B∶∠C=3∶5∶10,又△MNC≌△ABC,则∠BCM∶∠BCN等于( )

A. 1∶2 B. 1∶3 C. 2∶3 D. 1∶4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,tan∠CAB=2,则关于x的方程x2﹣5x+k=0的解为 .
的图象上运动,tan∠CAB=2,则关于x的方程x2﹣5x+k=0的解为 . 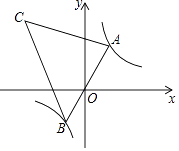
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
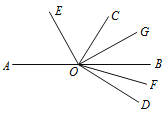
A. ∠DOG与∠BOE互补 B. ∠AOE-∠DOF=45°
C. ∠EOD与∠COG互补 D. ∠AOE与∠DOF互余
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
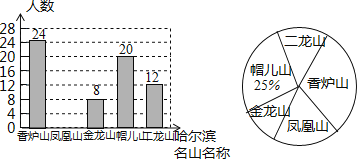
【题目】为贯彻落实十九大会议精神,践行“绿水青山就是金山银山”的发展理念,积极推动生态文明理念融入学校教育,某中学拟举办“爱家乡、览名山”活动,围绕“哈尔滨市周边五大名山,即:香炉山、凤凰山、金龙山、帽儿山、二龙山,你最喜欢那一座山?![]() 每名学生必选且只选一座山
每名学生必选且只选一座山![]() ”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整统计图
”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整统计图![]() 请根据统计图的信息回答下列问题:
请根据统计图的信息回答下列问题:
![]() 本次调查共抽取了多少名学生?
本次调查共抽取了多少名学生?
![]() 求本次调查中,最喜欢风凰山的学生人数,并补全条形统计图;
求本次调查中,最喜欢风凰山的学生人数,并补全条形统计图;
![]() 若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人.
若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com