
【题目】如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( ) 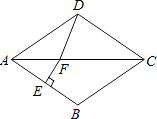
A.55°
B.65°
C.75°
D.85°
【答案】C
【解析】解:如图,连接BF, 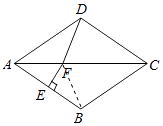
在菱形ABCD中,∠BAC= ![]() ∠BAD=
∠BAD= ![]() ×70°=35°,∠BCF=∠DCF,BC=DC,
×70°=35°,∠BCF=∠DCF,BC=DC,
∠ABC=180°﹣∠BAD=180°﹣70°=110°,
∵EF是线段AB的垂直平分线,
∴AF=BF,∠ABF=∠BAC=35°,
∴∠CBF=∠ABC﹣∠ABF=110°﹣35°=75°,
∵在△BCF和△DCF中,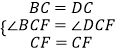 ,
,
∴△BCF≌△DCF(SAS),
∴∠CDF=∠CBF=75°,
故选C.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质和菱形的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为 . 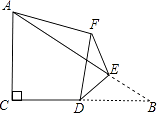
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某楼盘要对外销售![]() 该楼盘共23层,销售价格如下:第八层楼房售价为4000元
该楼盘共23层,销售价格如下:第八层楼房售价为4000元![]() 米
米![]() ,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,
,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,
![]() 请写出售价
请写出售价![]() 元
元![]() 米
米![]() 与楼层
与楼层![]() x取整数
x取整数![]() 之间的函数关系式.
之间的函数关系式.
![]() 已知该楼盘每套楼房面积均为100米
已知该楼盘每套楼房面积均为100米![]() ,若购买者一次性付清所有房款,开发商有两种优惠方案:
,若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价![]() ,另外每套楼房总价再减a元;
,另外每套楼房总价再减a元;
方案二:降价![]() .
.
老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s, 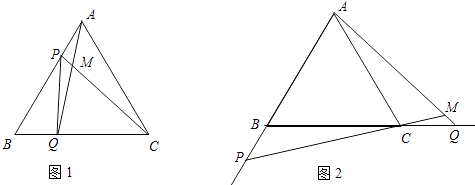
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)何时△PBQ是直角三角形?
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形![]() 中,
中,![]() ,点E、F分别在边AB、AC上,将
,点E、F分别在边AB、AC上,将![]() 沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且
沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且![]() .
.
![]() 求证:四边形AFDE是菱形.
求证:四边形AFDE是菱形.
![]() 若
若![]() ,
,![]() ,求线段ED的长度.
,求线段ED的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,边长为1的正方形OAP1B的顶点A、B分别在x轴、y轴上,点P1在反比例函数y= ![]() (x>0)的图象上,过P1A的中点B1作矩形B1AA1P2 , 使顶点P2落在反比例函数的图象上,再过P2A1的中点B2作矩形B2A1A2P3 , 使顶点P3落在反比例函数的图象上,…,依此规律,作出矩形Bn﹣1An﹣2An﹣1Pn时,落在反比例函数图象上的顶点Pn的坐标是 .
(x>0)的图象上,过P1A的中点B1作矩形B1AA1P2 , 使顶点P2落在反比例函数的图象上,再过P2A1的中点B2作矩形B2A1A2P3 , 使顶点P3落在反比例函数的图象上,…,依此规律,作出矩形Bn﹣1An﹣2An﹣1Pn时,落在反比例函数图象上的顶点Pn的坐标是 . 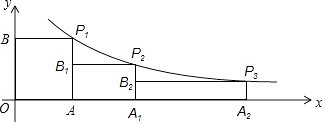
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABE≌△ADC≌△ABC,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( )
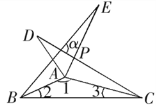
A. 80° B. 100° C. 60° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
平面直角坐标系中,矩形纸片OBCD按如图的方式放置![]() 已知
已知![]() ,
,![]() ,将这张纸片沿过点B的直
,将这张纸片沿过点B的直
线折叠,使点O落在边CD上,记作点A,折痕与边OD交于点E.
数学探究:
![]() 点C的坐标为______;
点C的坐标为______;
![]() 求点E的坐标及直线BE的函数关系式;
求点E的坐标及直线BE的函数关系式;
![]() 若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?
若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?
若存在,直接写出相应的点Q的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com