【题目】如图，在△ABC中，∠A∶∠B∶∠C=3∶5∶10，又△MNC≌△ABC，则∠BCM∶∠BCN等于（ ）
A. 1∶2 B. 1∶3 C. 2∶3 D. 1∶4
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，边长为1的正方形OAP1B的顶点A、B分别在x轴、y轴上，点P1在反比例函数y= 
（x＞0）的图象上，过P1A的中点B1作矩形B1AA1P2 ， 使顶点P2落在反比例函数的图象上，再过P2A1的中点B2作矩形B2A1A2P3 ， 使顶点P3落在反比例函数的图象上，…，依此规律，作出矩形Bn﹣1An﹣2An﹣1Pn时，落在反比例函数图象上的顶点Pn的坐标是 ．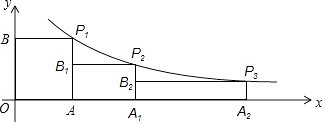 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，△ABE≌△ADC≌△ABC，若∠1∶∠2∶∠3=28∶5∶3，则∠α的度数为（ ）
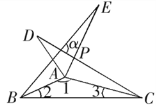
A. 80° B. 100° C. 60° D. 45°
查看答案和解析>>
科目：初中数学 来源： 题型：
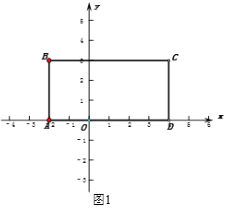
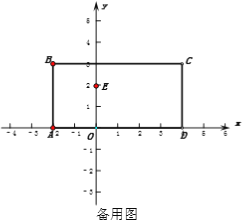
【题目】在平面直角坐标系中，如图1，第二象限内一点B（a，b），过B线段BA垂直于x轴，垂足为点A，实数a、b满足
，D（4，0），将线段AB向右平移使点A和点D重合得到线段DC,连接BC与y轴相交于点M.
（1）求点C的坐标；
（2）如图2,动点P从A点出发，沿折线AB-BC运动，运动到点C即停止运动，速度为每秒2个单位长度，设运动时间为t秒，当点P运动至线段BC上时，请用含有t的代数式表示在这一运动过程中线段PM的长，并直接写出t的取值范围；
（3）在（2）的条件下，y轴上有一点E（0，2），在点P在折线AB-BC运动过程中是否存在t值，使三角形PBE的面积为2，若存在，求出t值，并求出此时点P的坐标.
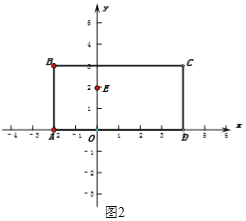
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知O为直线AB上一点，OC平分∠AOD，∠BOD=4∠DOE，∠COE=
，则∠BOE的度数为( )
A. 360°-4 B. 180°-4 C. D. 270°-3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知菱形ABCD在平面直角坐标系的位置如图所示，A（1，1），B（6，1），AC=4 
，点P是对角线OAC上的一个动点，E（0，2），当△EPD周长最小时，点P的坐标为（ ）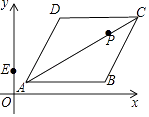 
A.（2，2）
B.（2， 
）
C.（ 
， 
）
D.（ 
， 
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境：
平面直角坐标系中，矩形纸片OBCD按如图的方式放置
已知
，
，将这张纸片沿过点B的直
线折叠，使点O落在边CD上，记作点A，折痕与边OD交于点E．
数学探究：
点C的坐标为______；
求点E的坐标及直线BE的函数关系式；
若点P是x轴上的一点，直线BE上是否存在点Q，能使以A，B，P，Q为顶点的四边形是平行四边形？
若存在，直接写出相应的点Q的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】公安人员在破案时常常根据案发现场作案人员留下的脚印推断犯人的身高，如果用a表示脚印长度，b表示身高，关系类似满足于：
（1）某人脚印长度为24.5cm，则他的身高约为多少？（精确到1cm）
（2）在某次案件中，抓获了两可疑人员，甲的身高为1.83m，乙的身高为1.89m，在现场测量的脚印为26.3cm，请你帮助侦察一下。哪个可疑人员的可能性更大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
