
����Ŀ��������Ա���ư�ʱ�������ݰ����ֳ�������Ա���µĽ�ӡ�ƶϷ��˵����ߣ������a��ʾ��ӡ���ȣ�b��ʾ���ߣ���ϵ���������ڣ�![]()
��1��ij�˽�ӡ����Ϊ24.5cm������������ԼΪ���٣�����ȷ��1cm��
��2����ij�ΰ����У�ץ������������Ա��������Ϊ1.83m���ҵ�����Ϊ1.89m�����ֳ������Ľ�ӡΪ26.3cm������������һ�¡��ĸ�������Ա�Ŀ����Ը���
���𰸡���1����������ԼΪ168cm����2������1.82m�ļ�����Ա�Ŀ����Ը���
��������
��1����a=24.5���������㼴�ɣ�
��2����a=26.3�������b=181.03cm��Ȼ����ݼס������˵�������181.03cm�Ľӽ��̶Ƚ����жϼ��ɣ�
��1����֪�����a��ʾ��ӡ���ȣ�b��ʾ���ߣ���ϵ���������ڣ�b=7a-3.07��
��ij�˽�ӡ����Ϊ24.5cm����a=24.5��
��������ϵʽ�ɵã�����ԼΪ7��24.5-3.07=168.43��168cm��
����������ԼΪ168cm��
��2�������ֳ������Ľ�ӡ����Ϊ26.3cm���������ֵ����b=7a-3.07�пɵã��ﷸ����Ϊ181.03cm��1.81cm���ȽϿ�֪������1.83m�ļ�����Ա�Ŀ����Ը���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A�á�B�á�C=3��5��10������MNC�ա�ABC�����BCM�á�BCN���ڣ� ��

A. 1��2 B. 1��3 C. 2��3 D. 1��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ABCD�У�F��AD���е㣬�ӳ�BC����E��ʹCE=
ABCD�У�F��AD���е㣬�ӳ�BC����E��ʹCE=![]() BC������DE��CF��
BC������DE��CF��

��1����֤���ı���CEDF��ƽ���ı��Σ�
��2����AB=4��AD=6����B=60������DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���RtABC �У���BAC=90������BC�Ͻ�ȡBD=BA������ABC��ƽ������AD�ཻ�ڵ�P������PC������ABC�����Ϊ8cm2������BPC�����Ϊ�� ��

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��k��0���뷴��������y= ![]() ��m��0����ͼ���й�����A��1��2����D����2����1����ֱ��l��x�ᣬ��x�ύ�ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�B��C��
��m��0����ͼ���й�����A��1��2����D����2����1����ֱ��l��x�ᣬ��x�ύ�ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�B��C�� 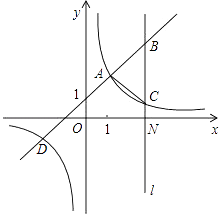
��1����һ�κ����뷴���������Ľ���ʽ��
��2�����ABC�������
��3������ͼ��ش���ʲô��Χʱ��һ�κ�����ֵ���ڷ�����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��D��E��BC���ϵĵ㣬����AD��AE���ԡ�ADE�ı�AE����ֱ��Ϊ�Գ�������ADE����Գ�ͼ�Ρ�AD��E������D��C����BD=CD�䣻
��1����֤����ABD�ա�ACD�䣻
��2������BAC=120�������DAE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��Բ��ĸ��OA������չ����õ�����AOC����֪Բ�ĸ�hΪ12cm��OA=13cm��������AOC�� ![]() �ij���cm�������������У���
�ij���cm����������������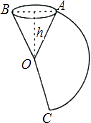
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
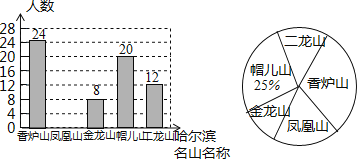
����Ŀ��Ϊ�᳹��ʵʮ�Ŵ���龫��������ˮ��ɽ���ǽ�ɽ��ɽ���ķ�չ��������ƶ���̬������������ѧУ������ij��ѧ��ٰ��������硢����ɽ�����Χ�������������ܱ������ɽ��������¯ɽ�����ɽ������ɽ��ñ��ɽ������ɽ������ϲ����һ��ɽ��![]() ÿ��ѧ����ѡ��ֻѡһ��ɽ
ÿ��ѧ����ѡ��ֻѡһ��ɽ![]() ����������ȫУ��Χ�������ȡ�˲���ѧ�������ʾ����飬���ݵ�������������ͼ��ʾ�IJ�����ͳ��ͼ
����������ȫУ��Χ�������ȡ�˲���ѧ�������ʾ����飬���ݵ�������������ͼ��ʾ�IJ�����ͳ��ͼ![]() �����ͳ��ͼ����Ϣ�ش��������⣺
�����ͳ��ͼ����Ϣ�ش��������⣺
![]() ���ε��鹲��ȡ�˶�����ѧ����
���ε��鹲��ȡ�˶�����ѧ����
![]() �ε����У���ϲ�����ɽ��ѧ������������ȫ����ͳ��ͼ��
�ε����У���ϲ�����ɽ��ѧ������������ȫ����ͳ��ͼ��
![]() ������ѧ����ѧ��1200�ˣ�������Ƹ���ѧ��ϲ����¯ɽ��ѧ��Լ�ж����ˣ�
������ѧ����ѧ��1200�ˣ�������Ƹ���ѧ��ϲ����¯ɽ��ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������������ֱ�Ϊ����2��8��������11��6��������14��0������0��0����
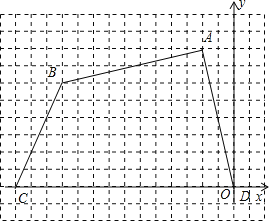
��1��������ı��ε������
��2�������ԭ�����ı���ABCD����ƽ��3����λ���ȣ�������ƽ��2����λ���Ⱥ�õ��µ��ı���A1B2C3D4����ֱ��д��ƽ�ƺ���ı��θ������������ı��ε������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com