
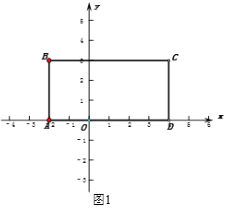
【题目】在平面直角坐标系中,如图1,第二象限内一点B(a,b),过B线段BA垂直于x轴,垂足为点A,实数a、b满足![]() ,D(4,0),将线段AB向右平移使点A和点D重合得到线段DC,连接BC与y轴相交于点M.
,D(4,0),将线段AB向右平移使点A和点D重合得到线段DC,连接BC与y轴相交于点M.
(1)求点C的坐标;
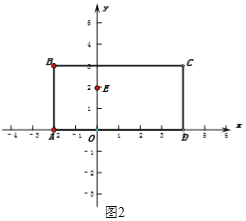
(2)如图2,动点P从A点出发,沿折线AB-BC运动,运动到点C即停止运动,速度为每秒2个单位长度,设运动时间为t秒,当点P运动至线段BC上时,请用含有t的代数式表示在这一运动过程中线段PM的长,并直接写出t的取值范围;
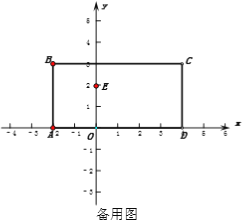
(3)在(2)的条件下,y轴上有一点E(0,2),在点P在折线AB-BC运动过程中是否存在t值,使三角形PBE的面积为2,若存在,求出t值,并求出此时点P的坐标.
【答案】(1)C(4,3);(2)PM=5-2t(![]() ≤t<
≤t<![]() );PM=2t-5(
);PM=2t-5(![]() <t≤
<t≤![]() );(3)t=
);(3)t=![]() 或
或![]() 时,△PBE的面积为2,P点的坐标为(-2,1)和(2,3).
时,△PBE的面积为2,P点的坐标为(-2,1)和(2,3).
【解析】
(1)根据非负数之和求出a,b易知C点坐标.
(2) 讨论点P在BM上,点P在CM上,根据BM,CM长度可算出PM的长度.
(3) 讨论当点P在线段AB上,当点P在线段BC上时,分别求出t值和P点坐标即可.
解:(1)∵![]() ≥0,
≥0, ![]() ≥0
≥0
又∵![]() ,
,
∴![]() =0,
=0,![]() =0
=0
∴![]()
∴B(-2,3),A(-2,0)
又∵线段AB向右平移使点A和点D重合得到线段DC,D(4,0)
∴点C与点B对应 即C(4,3)
(2)由(1)得,AB=3,BC=AD=6,设BC与y轴相交于点M,
∵BC∥x轴
∴M(0,3)
∴BM=2,MC=4
当点P在BM上时,即![]() ≤t<
≤t<![]()
PM=5-2t
当点P在CM上时,即![]() <t≤
<t≤![]()
PM=2t-5
(3)有两种情况:
情况一:当点P在线段AB上
∵![]() PB·BM=2
PB·BM=2
∴BM=2
∴BP=2
∴ AP=AB-BP=1 即2t=1,t=![]() ,
,
此时P(-2,1)情况二,当点P在线段BC上时
∵![]() PB·BM=2
PB·BM=2
∴BM=1
∴BP=4
∴2t-3=4,t=![]()
此时P(2,3)
综上,当t=![]() 或
或![]() 时,△PBE的面积为2,此时P点的坐标为(-2,1)和(2,3).
时,△PBE的面积为2,此时P点的坐标为(-2,1)和(2,3).


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=![]() ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
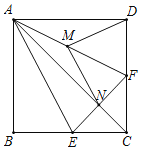
【题目】操作与证明:如图,把一个含![]() 角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、
角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、![]() 其中AC与EF交于点N,取AF中点M,连接MD、MN.
其中AC与EF交于点N,取AF中点M,连接MD、MN.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 在
在![]() 的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y= ![]() 图象恰好过点D,则k的值为( )
图象恰好过点D,则k的值为( ) 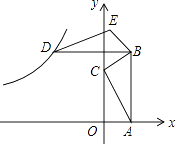
A.6
B.﹣6
C.9
D.﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A∶∠B∶∠C=3∶5∶10,又△MNC≌△ABC,则∠BCM∶∠BCN等于( )

A. 1∶2 B. 1∶3 C. 2∶3 D. 1∶4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。
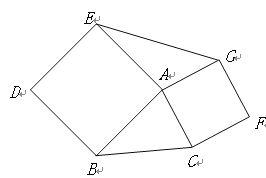
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
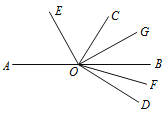
A. ∠DOG与∠BOE互补 B. ∠AOE-∠DOF=45°
C. ∠EOD与∠COG互补 D. ∠AOE与∠DOF互余
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,2),D(﹣2,﹣1).直线l⊥x轴,与x轴交于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2),D(﹣2,﹣1).直线l⊥x轴,与x轴交于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C. 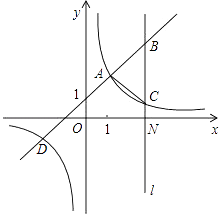
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积;
(3)根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com