
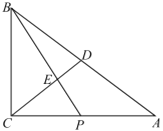
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,
上一动点,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)如果![]() ,
,![]() ,且
,且![]() 为
为![]() 的中点,求线段
的中点,求线段![]() 的长;
的长;
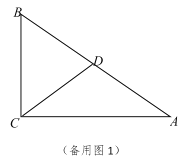
(2)联结![]() ,如果
,如果![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
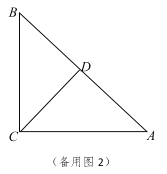
(3)联结![]() ,如果
,如果![]() ,且
,且![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据已知条件得到CP=4,求得BP=2![]() ,根据三角形重心的性质即可得到结论;
,根据三角形重心的性质即可得到结论;
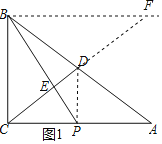
(2)如图1,过点B作BF∥CA交CD的延长线于点F,根据平行线分线段成比例定理得到![]() ,求得
,求得![]() ,设CP=k,则PA=3k,得到PA=PB=3k根据三角函数的定义即可得到结论;
,设CP=k,则PA=3k,得到PA=PB=3k根据三角函数的定义即可得到结论;
(3)根据直角三角形的性质得到CD=BD=![]() AB,推出△PBD∽△ABP,根据相似三角形的性质得到∠BPD=∠A,推出△DPE∽△DCP,根据相似三角形的性质即可得到结论.
AB,推出△PBD∽△ABP,根据相似三角形的性质得到∠BPD=∠A,推出△DPE∽△DCP,根据相似三角形的性质即可得到结论.
解:(1)∵![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
∵![]() 是边
是边![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
∴点![]() 是
是![]() 的重心
的重心
∴![]()
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]()
∴![]()
∵![]() ,∴
,∴![]() ,
,![]()
∵![]() ,
,![]() ,则
,则![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]()
∵![]() ,
,![]() 是边
是边![]() 的中点,∴
的中点,∴![]()
∴![]() ,∴
,∴![]() ,∵
,∵![]()
∴![]()
(3)∵![]() ,
,![]() 是边
是边![]() 的中点
的中点
∴![]()
∵![]()
∴![]()
∵![]() ,∴
,∴![]()
∴![]()
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
![]() ,∴
,∴![]()
∵![]() ,
,![]() ,∴
,∴![]()


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
科目:初中数学 来源: 题型:
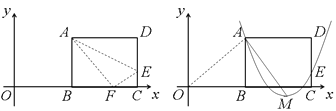
【题目】如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.
(1)求点E、F的坐标(用含m的式子表示);(5分)
(2)连接OA,若△OAF是等腰三角形,求m的值;(4分)
(3)如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值. (5分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在线段AB上,AO=2OB=2![]() ,
,![]() ,点C是射线OP上的一个动点.
,点C是射线OP上的一个动点.
(1)如图①,当![]() ,OC=2,求
,OC=2,求![]() 的值;
的值;
(2)如果②,当AC=AB时,求OC的长(用含![]() 的代数式表示);
的代数式表示);
(3)在第(2)题的条件下,过点A作AQ//BC,并使![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:
当a>0,b>0时:
∵(![]() )2=a﹣2
)2=a﹣2![]() +b≥0
+b≥0
∴a+b≥2![]() ,当且仅当a=b时取等号.
,当且仅当a=b时取等号.
请利用上述结论解决以下问题:
(1)请直接写出答案:当x>0时,x+![]() 的最小值为 .当x<0时,x+
的最小值为 .当x<0时,x+![]() 的最大值为 ;
的最大值为 ;
(2)若y=![]() ,(x>﹣1),求y的最小值;
,(x>﹣1),求y的最小值;
(3)如图,四边形ABCD的对角线AC、BD相交于点O,△AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
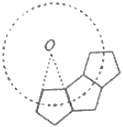
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,点E是斜边AB的中点,AB=10,BC=8,点P在CE的延长线上,过点P作PQ⊥CB,交CB的延长线于点Q,设EP=x
(1)如图1,求证:△ABC∽△PCQ;
(2)如图2,连接PB,当PB平分∠CPQ时,试用含x的代数式表示△PBE的面积;
(3)如图3,过点B作BF⊥AB交PQ于点F.若∠BEF=∠A,试求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是BD的中点,CE⊥AB,垂足为E,BD交CE于点F.

【1】求证:CF=BF;
【2】若AD=2,⊙O的半径为3,求BC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com