
ЁОЬтФПЁПAЪазМБИељДДШЋЙњЮРЩњГЧЪаЃЎФГаЁЧјЛ§МЋЯьгІЃЌОіЖЈдкаЁЧјФкАВзАРЌЛјЗжРрЕФЬсЪОХЦКЭРЌЛјЯфЃЌШєЙКТђ2ИіЬсЪОХЦКЭ3ИіРЌЛјЯфЙВаш550дЊЃЌЧвРЌЛјЯфЕФЕЅМлЪЧЬсЪОХЦЕЅМлЕФ3БЖЃЎ
ЃЈ1ЃЉЧѓЬсЪОХЦКЭРЌЛјЯфЕФЕЅМлИїЪЧЖрЩйдЊ?
ЃЈ2ЃЉИУаЁЧјжСЩйашвЊАВЗХ48ИіРЌЛјЯфЃЌШчЙћЙКТђЬсЪОХЦКЭРЌЛјЯфЙВ100ИіЃЌЧвЗбгУВЛГЌЙ§10000дЊЃЌЧыФуСаОйГіЫљгаЙКТђЗНАИЃЎ
ЁОД№АИЁПЃЈ1ЃЉ50дЊЃЌ150дЊЃЛЃЈ2ЃЉЬсЪОХЦ50ИіЃЌРЌЛјЯф50ИіЃЛЬсЪОХЦ51ИіЃЌРЌЛјЯф49ИіЃЛЬсЪОХЦ52ИіЃЌРЌЛјЯф48ИіЃЛ
ЁОНтЮіЁП
1ЃЉИљОнЁАЙКТђ2ИіЬсЪОХЦКЭ3ИіРЌЛјЯфЙВаш550дЊЁБЃЌНЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉИљОнЁАЗбгУВЛГЌЙ§10000дЊКЭжСЩйашвЊАВЗХ48ИіРЌЛјЯфЁБЃЌНЈСЂВЛЕШЪНМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЩшЬсЪОХЦЕФЕЅМлЮЊ![]() дЊЃЌдђРЌЛјЯфЕФЕЅМлЮЊ
дЊЃЌдђРЌЛјЯфЕФЕЅМлЮЊ![]() дЊЃЌ
дЊЃЌ
ИљОнЬтвтЕУЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
МДЃКЬсЪОХЦКЭРЌЛјЯфЕФЕЅМлИїЪЧ50дЊКЭ150дЊЃЛ
ЃЈ2ЃЉЩшЙКТђЬсЪОХЦ![]() Иі
Иі![]() ЮЊе§ећЪ§ЃЉЃЌдђРЌЛјЯфЮЊ
ЮЊе§ећЪ§ЃЉЃЌдђРЌЛјЯфЮЊ![]() ИіЃЌ
ИіЃЌ
ИљОнЬтвтЕУЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЮЊе§ећЪ§ЃЌ
ЮЊе§ећЪ§ЃЌ
![]() ЮЊ50ЃЌ51ЃЌ52ЃЌЙВ3жжЗНАИЃЛ
ЮЊ50ЃЌ51ЃЌ52ЃЌЙВ3жжЗНАИЃЛ
МДЃКЮТмАЬсЪОХЦ50ИіЃЌРЌЛјЯф50ИіЃЛЮТмАЬсЪОХЦ51ИіЃЌРЌЛјЯф49ИіЃЛЮТмАЬсЪОХЦ52ИіЃЌРЌЛјЯф48ИіЃЌ


 гЂгяаЁгЂалЬьЬьФЌаДЯЕСаД№АИ
гЂгяаЁгЂалЬьЬьФЌаДЯЕСаД№АИ ЪюМйзївЕАВЛеЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
ЪюМйзївЕАВЛеЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОХФъШ§АрЕФаЁгъЭЌбЇЯыСЫНтБОаЃОХФъМЖбЇЩњЖдФФУХПЮГЬИааЫШЄЃЌЫцЛњГщШЁСЫВПЗжОХФъМЖбЇЩњНјааЕїВщЃЈУПУћбЇЩњБижЛФмбЁдёвЛУХПЮГЬЃЉЃЎНЋЛёЕУЕФЪ§ОнећРэЛцжЦШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкетДЮЕїВщжавЛЙВГщШЁСЫЁЁ ЁЁУћбЇЩњЃЌmЕФжЕЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉЧыИљОнОнвдЩЯаХЯЂжБдкД№ЬтПЈЩЯВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉЩШаЮЭГМЦЭМжаЃЌЁАЪ§бЇЁБЫљЖдгІЕФдВаФНЧЖШЪ§ЪЧЁЁ ЁЁЖШЃЛ
ЃЈ4ЃЉШєИУаЃОХФъМЖЙВга1000УћбЇЩњЃЌИљОнГщбљЕїВщЕФНсЙћЃЌЧыФуЙРМЦИУаЃОХФъМЖбЇЩњжагаЖрЩйУћбЇЩњЖдЪ§бЇИааЫШЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈЉ3ЃЌ5ЃЉЃЌBЃЈЉ2ЃЌ1ЃЉЃЌCЃЈЉ1ЃЌ3ЃЉ.
ЃЈ1ЃЉШєЁїABCКЭЁїA1B1C1ЙигкxжсГЩжсЖдГЦЃЌЛГіЁїA1B1C1
ЃЈ2ЃЉЕуC1ЕФзјБъЮЊ_________,ЁїABCЕФУцЛ§ЮЊ__________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊГЄЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌгЩ
ЩЯЃЌгЩ![]() Эљ
Эљ![]() дЫЖЏЃЌЫйЖШЮЊ
дЫЖЏЃЌЫйЖШЮЊ![]() ЃЌдЫЖЏЪБМфЮЊ
ЃЌдЫЖЏЪБМфЮЊ![]() УыЃЌНЋ
УыЃЌНЋ![]() бизХ
бизХ![]() ЗелжС
ЗелжС![]() ЃЌЕу
ЃЌЕу![]() ЖдгІЕуЮЊ
ЖдгІЕуЮЊ![]() ЃЌ
ЃЌ![]() ЫљдкжБЯпгыБп
ЫљдкжБЯпгыБп![]() НЛгыЕу
НЛгыЕу![]() ЃЌ
ЃЌ
ЃЈ1ЃЉШчЭМ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧѓжЄЃК
ЪБЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊКЮжЕЪБЃЌЕу
ЮЊКЮжЕЪБЃЌЕу![]() ЧЁКУТфдкБп
ЧЁКУТфдкБп![]() ЩЯЃЛ
ЩЯЃЛ
ЃЈ3ЃЉШчЭМ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаЕРТЗУРЛЏЙЄГЬеаБъЃЌОВтЫуЃКМзЖг 12 ЬьЭъГЩЕФЙЄГЬСПЪЧввЖг 9 ЬьЭъГЩЕФЙЄГЬСПЕФ2 БЖЃЌМзЖгИЩ 20 ЬьБШввЖгИЩ 15 ЬьЖрЭъГЩЕФЙЄГЬСПеМзмЙЄГЬСПЕФ![]() .
.
ЃЈ1ЃЉЧѓМзЁЂввСНЖгвЛЬьИїЭъГЩДЫЯюЙЄГЬЕФСПЃП
ЃЈ2ЃЉМзЖгЪЉЙЄвЛЬьашИЖЙЄГЬПю 1.5 ЭђдЊЃЌввЖгЪЉЙЄвЛЬьашИЖЙЄГЬПю 0.8 ЭђдЊЃЌШєвЊЧѓЭъГЩДЫЯюЙЄГЬЕФЙЄГЬПюВЛГЌЙ§ 81 ЭђдЊЃЌдђввЖгзюЩйЪЉЙЄЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКУбЇЕФаЁКьдкбЇЭъШ§НЧаЮЕФНЧЦНЗжЯпКѓЃЌгіЕНЯТСа4ИіЮЪЬтЃЌЧыФуАяЫ§НтОіЃЎШчЭМЃЌдк![]() жаЃЌЕу
жаЃЌЕу![]() ЪЧ
ЪЧ![]() ЁЂ
ЁЂ![]() ЕФЦНЗжЯпЕФНЛЕуЃЌЕу
ЕФЦНЗжЯпЕФНЛЕуЃЌЕу![]() ЪЧ
ЪЧ![]() ЁЂ
ЁЂ![]() ЦНЗжЯпЕФНЛЕуЃЌ
ЦНЗжЯпЕФНЛЕуЃЌ![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЎ
ЃЎ

ЃЈ1ЃЉШє![]() ЃЌдђ
ЃЌдђ![]() ЁуЃЛ
ЁуЃЛ
ЃЈ2ЃЉШє![]() ЃЈ
ЃЈ![]() ЃЉЃЌдђЕБ
ЃЉЃЌдђЕБ![]() ЕШгкЖрЩйЖШЃЈгУКЌ
ЕШгкЖрЩйЖШЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЪБЃЌ
ЕФДњЪ§ЪНБэЪОЃЉЪБЃЌ![]() ЃЌВЂЫЕУїРэгЩЃЛ
ЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
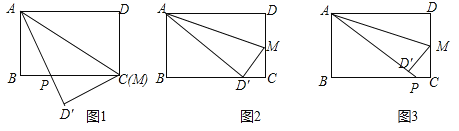
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDКЭЫФБпаЮDEFGЖМЪЧе§ЗНаЮЃЌЕуEЃЌGЗжБ№дкADЃЌCDЩЯЃЌСЌНгAFЃЌBFЃЌCFЃЎ
ЃЈ1ЃЉЧѓжЄЃКAF=CFЃЛ
ЃЈ2ЃЉШєЁЯBAF=35ЁуЃЌЧѓЁЯBFCЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯMON=30ЁуЃЌBЮЊOMЩЯвЛЕуЃЌBAЁЭONгкAЃЌЫФБпаЮABCDЮЊе§ЗНаЮЃЌPЮЊЩфЯпBMЩЯвЛЖЏЕуЃЌСЌНсCPЃЌНЋCPШЦЕуCЫГЪБеыЗНЯђа§зЊ90ЁуЕУCEЃЌСЌНсBEЃЌШєAB=4ЃЌдђBEЕФзюаЁжЕЮЊ ЃЎ 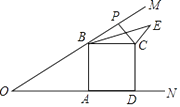
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќжБНЧШ§НЧаЮABDжаЃЌAD=BDЃЌЕуFЪЧADЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуAзїACЁЭBFЃЌНЛBFЕФбгГЄЯпгкЕуEЃЌНЛBDЕФбгГЄЯпгкЕуCЃЌдђЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
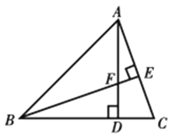
A.CD=DFB.AC=BFC.AD=BED.ЁЯCAD+ЁЯABF=45Ёу
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com