
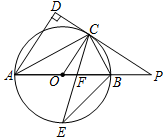
 如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.分析 (1)根据切线的性质得OC⊥AD,而AD⊥DP,则肯定判断OC∥AD,根据平行线的性质得∠DAC=∠OCA,加上∠OAC=∠OCA,所以∠OAC=∠DAC;
(2)根据圆周角定理由AB为⊙O的直径得∠ACB=90°,则∠BCE=45°,再利用圆周角定理得∠BOE=2∠BCE=90°,则∠OFE+∠OEF=90°,易得∠CFP+∠OEF=90°,再根据切线的性质得到∠OCF+∠PCF=90°,而∠OCF=∠OEF,根据等角的余角相等得到∠PCF=∠CFP,于是可判断△PCF是等腰三角形;
(3)连结OE.由AB为⊙O的直径,得到∠ACB=90°,根据角平分线的定义得到∠BCE=45°,设⊙O 的半径为r,则OF=6-r,根据勾股定理列方程即可得到结论.
解答 (1)证明:∵PD为⊙O的切线,
∴OC⊥DP,
∵AD⊥DP,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=∠DAC,
∴AC平分∠DAB;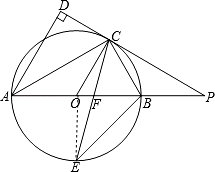 (2)证明:∵AB为⊙O的直径,
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵CE平分∠ACB,
∴∠BCE=45°,
∴∠BOE=2∠BCE=90°,
∴∠OFE+∠OEF=90°,
而∠OFE=∠CFP,
∴∠CFP+∠OEF=90°,
∵OC⊥PD,
∴∠OCP=90°,即∠OCF+∠PCF=90°,
而∠OCF=∠OEF,
∴∠PCF=∠CFP,
∴△PCF是等腰三角形;
(3)解:连结OE.
∵AB为⊙O的直径,∴∠ACB=90°,
∵CE平分∠ACB,∴∠BCE=45°,
∴∠BOE=90°,即OE⊥AB,
设⊙O 的半径为r,则OF=6-r,
在Rt△EOF中,∵OE2+OF2=EF2,
∴r2+(6-r)2=(2$\sqrt{5}$)2,
解得,r1=4,r2=2,
当r1=4时,OF=6-r=2(符合题意),
当r2=2时,OF=6-r=4(不合题意,舍去),
∴⊙O的半径r=4.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和等腰三角形的判定.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com