解:(1)原式=2x
3-3x
2-3+x
3-4x
2=3x
3-7x
2-3,
当x=-1时,原式=3×(-1)-7×1-3=-13;
(2)∵

,
∴a+2=0,b-

=0,
∴a=-2,b=

,
原式=5a
2b-2a
2b+ab
2-2a
2b+4-2ab
2=a
2b-ab
2+4,
当a=-2,b=

,原式=4×

-(-2)×

+4=6

;
(3)原式=-

(a-b)
2-4(a-b),
当a-b=2时,原式=-

×4-4×2=-9;
(4)∵0.5x
|a|y
4与
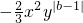
是同类项,
∴|a|=2,|b-1|=4,
∴a=±2,b=5或-3,
又∵a>b,
∴a=2,b=-3;a=-2,b=-3,
原式=-a
2-

ab+

b
2,
当a=2,b=-3时,原式=-4-

×(-6)+

×9=5,
当a=-2,b=-3时,原式=-4-

×6+

×9=-1.
分析:(1)先将原式去括号、合并同类项,再把x=-1代入化简后的式子,计算即可;
(2)根据两个非负数的和等于0,可知每一个非负数等于0,可求出a、b的值,再对所求代数式化简,然后再把a、b的值代入化简后的式子,计算即可;
(3)先合并同类项,再把a-b的值整体代入化简后的式子计算即可;
(4)先根据同类项的定义,以及a>b,可求出两组a、b的值,分别代入化简后的式子,计算即可.
点评:本题考查了整式的化简求值、非负数的性质、同类项的定义.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.

 ,求5a2b-[2a2b-(ab2-2a2b)-4]-2ab2的值;
,求5a2b-[2a2b-(ab2-2a2b)-4]-2ab2的值; 的值;
的值;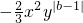 是同类项,且a>b,求
是同类项,且a>b,求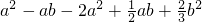 的值.
的值. ,
, =0,
=0, ,
, ,原式=4×
,原式=4× -(-2)×
-(-2)× +4=6
+4=6 ;
; (a-b)2-4(a-b),
(a-b)2-4(a-b), ×4-4×2=-9;
×4-4×2=-9;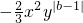 是同类项,
是同类项, ab+
ab+ b2,
b2, ×(-6)+
×(-6)+ ×9=5,
×9=5, ×6+
×6+ ×9=-1.
×9=-1.

 阅读快车系列答案
阅读快车系列答案