
 如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).分析 (1)首先过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,可得△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,则可求得BN=$\sqrt{2}$b,DM=$\sqrt{2}$a,继而求得答案;
(2)由S△AMN=S△ABD-S△ABM-S△ADN,可得S△AMN=$\frac{1}{2}$c2-$\frac{1}{2}$c(c-a)-$\frac{1}{2}$c(c-b),继而求得答案;
(3)易证得∴∠DMA=∠BAN,又由∠ABD=∠ADB=45°,可证得△ADM∽△NBA,然后由相似三角形的对应边成比例,求得答案.
解答 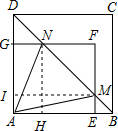 (1)证明:过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,
(1)证明:过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°,
∴△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,
∴BN=$\sqrt{2}$NH=$\sqrt{2}$AG=$\sqrt{2}$b,DM=$\sqrt{2}$MI=$\sqrt{2}$AE=$\sqrt{2}$a,
∴:$\frac{BN}{DM}$=$\frac{b}{a}$;
(2)S△AMN=S△ABD-S△ABM-S△ADN
=$\frac{1}{2}$AB•AD-$\frac{1}{2}$AB•ME-$\frac{1}{2}$AD•NG
=$\frac{1}{2}$c2-$\frac{1}{2}$c(c-a)-$\frac{1}{2}$c(c-b)
=$\frac{1}{2}$c(c-c+a-c+b)
=$\frac{1}{2}$c(a+b-c);
(3)∵∠DMA=∠ABD+∠MAB=∠MAB+45°,∠BAN=∠MAB+∠MAN=∠MAB+45°,
∴∠DMA=∠BAN,
∵∠ABD=∠ADB=45°,
∴△ADM∽△NBA,
∴$\frac{DM}{AD}$=$\frac{AB}{BN}$,
∵DM=$\sqrt{2}$a,BN=$\sqrt{2}$b,
∴c2=2ab.
点评 此题属于四边形的综合题.考查了正方形的性质、等腰直角三角形的性质以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于二次函数y=x2-(4k+2)x+4k2+3k的图象与x轴有两个交点.
已知关于二次函数y=x2-(4k+2)x+4k2+3k的图象与x轴有两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读理解:
阅读理解:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com