
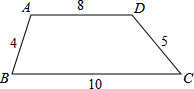
 在四边形ABCD中,AD∥BC,AB与CD不平行,根据图中数据,若BA、CD延长后交于点M,则△MBC的周长为55.
在四边形ABCD中,AD∥BC,AB与CD不平行,根据图中数据,若BA、CD延长后交于点M,则△MBC的周长为55. 分析 由AD∥BC,得到△ADM∽△BCM,根据对应线段成比例列出方程$\frac{MA}{MB}$=$\frac{MD}{MC}$=$\frac{AD}{BC}$=$\frac{8}{10}$=$\frac{4}{5}$,解出MB=20,MC=25,由三角形的周长公式求出答案.
解答 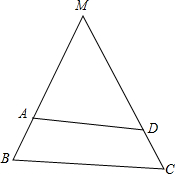 解:如图,∵AD∥BC,
解:如图,∵AD∥BC,
∴△ADM∽△BCM,
∴$\frac{MA}{MB}$=$\frac{MD}{MC}$=$\frac{AD}{BC}$=$\frac{8}{10}$=$\frac{4}{5}$,
∴AM=16,MD=20,
∴MB=20,MC=25,
∴△MBC的周长=20+10+25=55.
故答案为:55.
点评 本题考查了相似三角形的判定和性质,三角形的周长的求法,正确的找准对应线段是解题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
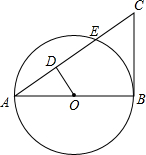 如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
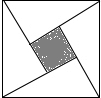 由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )| A. | 1 | B. | 3 | C. | 4-2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com