
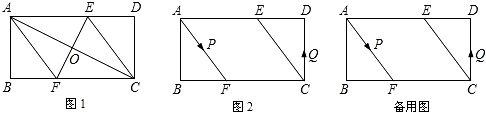
分析 (1)先证明四边形ABCD为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;
(2)根据勾股定理即可求AF的长;
(2)分情况讨论可知,P点在BF上,Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可.
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,
∴OA=OC,
∵在△AOE和△COF中,
$\left\{\begin{array}{l}{∠CAD=∠ACB}\\{∠AEF=∠CFE}\\{OA=OC}\end{array}\right.$
∴△AOE≌△COF(AAS),
∴OE=OF(AAS),
∵EF⊥AC,
∴四边形AFCE为菱形;
(2)设菱形的边长AF=CF=xcm,则BF=(8-x)cm,
在Rt△ABF中,AB=4cm,由勾股定理,得
16+(8-x)2=x2,
解得:x=5,
∴AF=5;
(2)由作图可以知道,P点AF上时,Q点CD上,此时A,C,P,Q四点不可能构成平行四边形,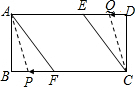
同理P点AB上时,Q点DE或CE上,也不能构成平行四边形,
∴只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,
∴PC=QA,
∵点P的速度为每秒2cm,点Q的速度为每秒1.2cm,运动时间为t秒,
∴PC=2t,QA=12-1.2t,
∴2t=12-1.2t,
解得:t=$\frac{15}{4}$,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t=$\frac{15}{4}$秒.
点评 本题考查了矩形的性质的运用,菱形的判定及性质的运用,勾股定理的运用,平行四边形的判定及性质的运用,解答时分析清楚动点在不同的位置所构成的图形的形状是解答本题的关键


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:填空题
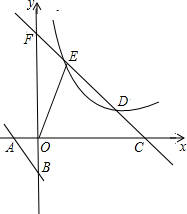 如图,直线l:y=-2x-2与x轴、y轴分别交于A、B两点,向右平移直线l交第一象限内双曲线y=$\frac{k}{x}$于D、E,交x轴正半轴于C,CD交y轴于F点,若CD=AB,S△EOC=12,则k的值为6.
如图,直线l:y=-2x-2与x轴、y轴分别交于A、B两点,向右平移直线l交第一象限内双曲线y=$\frac{k}{x}$于D、E,交x轴正半轴于C,CD交y轴于F点,若CD=AB,S△EOC=12,则k的值为6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
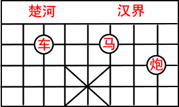 如图,已知棋子“车”的坐为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
如图,已知棋子“车”的坐为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )| A. | (2,3) | B. | (3,2) | C. | (-2,-3) | D. | (-3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
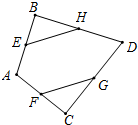 如图,在四边形ABCD中,AB=AC,DB⊥AB,DC⊥AC,且E,F,G,H分别为AB,AC,CD,BD的中点.
如图,在四边形ABCD中,AB=AC,DB⊥AB,DC⊥AC,且E,F,G,H分别为AB,AC,CD,BD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com