
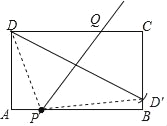
【题目】如图矩形ABCD中AB=6,AD=4,点P为AB上一点,把矩形ABCD沿过P点的直线l折叠,使D点落在BC边上的D′处,直线l与CD边交于Q点.
(1)在图(1)中利用无刻度的直尺和圆规作出直线l.(保留作图痕迹,不写作法和理由)
(2)若PD′⊥PD,①求线段AP的长度;②求sin∠QD′D.

【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意作出图形即可;
(2)由(1)知,PD=PD′,根据余角的性质得到∠ADP=∠BPD′,根据全等三角形的性质得到AD=PB=4,得到AP=2;根据勾股定理得到PD=![]() =2
=2![]() ,CD′=
,CD′=![]() =2,根据三角函数的定义即可得到结论.
=2,根据三角函数的定义即可得到结论.
(1)连接PD,以P为圆心,PD为半径画弧交BC于D′,过P作DD′的垂线交CD于Q,
则直线PQ即为所求;
(2)由(1)知,PD=PD′,
∵PD′⊥PD,
∴∠DPD′=90°,
∵∠A=90°,
∴∠ADP+∠APD=∠APD+∠BPD′=90°,
∴∠ADP=∠BPD′,
在△ADP与△BPD′中,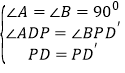 ,
,
∴△ADP≌△BPD′,
∴AD=PB=4,
∵PB=AB﹣AP=6﹣AP=4,
∴AP=2;
∴PD=![]() =2
=2![]() ,
,
∵PD=PD′,PD⊥PD′,
∵DD′=![]() PD=2
PD=2![]() ,
,
∴CD′=![]() =2,
=2,
∴sin∠QD′D=sin∠QDD′=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴![]() ,∴a=2,b=1
,∴a=2,b=1
∴![]() =
=![]() =
=![]() +
+![]() =x2+2+
=x2+2+![]() 这样,分式
这样,分式![]() 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)试说明![]() 的最小值为8.
的最小值为8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强在做课后习题时,遇到这样一道题:“如图所示,![]() 、
、![]() 两村庄在一条河的两岸,从
两村庄在一条河的两岸,从![]() 村庄去
村庄去![]() 村庄,需要在河上造一座桥
村庄,需要在河上造一座桥![]() ,请问桥造在何处从
,请问桥造在何处从![]() 村庄去
村庄去![]() 村庄的路径最短?(假定河的两岸是平行的直线,桥与河垂直)”
村庄的路径最短?(假定河的两岸是平行的直线,桥与河垂直)”
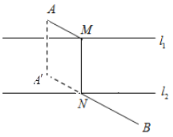
小强的解题思路,因为桥与河岸垂直,线段![]() 是一个不变的量,将它平移到
是一个不变的量,将它平移到![]() 处得线段
处得线段![]() ,总的路程
,总的路程![]() 与
与![]() 是相等的,故要使
是相等的,故要使![]() 最短,就是求点
最短,就是求点![]() 到点
到点![]() 最短即可,所以点
最短即可,所以点![]() 应是
应是![]() 与
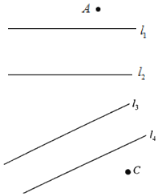
与![]() 的交点.根据上述材料解答下列问题:如图所示:
的交点.根据上述材料解答下列问题:如图所示:![]() 、
、![]() 两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从
两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从![]() 地出发到
地出发到![]() 地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短?(假定河的两岸是平行的直线,河
地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短?(假定河的两岸是平行的直线,河![]() 与
与![]() 的宽为
的宽为![]() ,河
,河![]() 与
与![]() 的宽为
的宽为![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
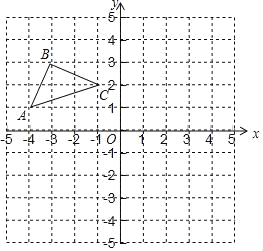
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个顶点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标:A1( ),B1( ),C1( );
(2)画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2,连接C1C2,CC2,C1C,并直接写出△CC1C2的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为5,l2与l3的距离为7,则Rt△ABC的面积为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一副三角板按如图所示的方式放置,则下列结论:①![]() ;②如果
;②如果![]() ,则有
,则有![]() ;③如果
;③如果![]() ,则有
,则有![]() ;④如果
;④如果![]() ,必有
,必有![]() ;其中正确的有( )
;其中正确的有( )
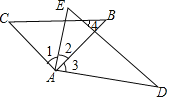
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“ a 2 ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
x2 4x 5 x2 4x 4 1 x 22 1 ,
∵ x 22 ≥0,
∴ x 22 1 ≥1,
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题:
(1)填空: x2 4x 5 ( x )2+ ;
(2)已知 x2 4x y2 2y 5 0 ,求 x y 的值;
(3)比较代数式 x2 1与2x 3 的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com