Question

【题目】如图，菱形ABCD中，AB=AC，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，连接DH交AG于点O．则下列结论①△ABF≌△CAE，②∠AHC=120°，③AH+CH=DH中，正确的是（ ）

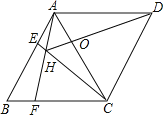
A．①② B．①③ C．②③ D．①②③

Answer 1

【答案】D

【解析】

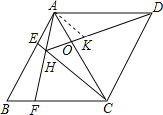
试题分析：由菱形ABCD中，AB=AC，易证得△ABC是等边三角形，则可得∠B=∠EAC=60°，由SAS即可证得△ABF≌△CAE；则可得∠BAF=∠ACE，利用三角形外角的性质，即可求得∠AHC=120°；在HD上截取HK=AH，连接AK，易得点A，H，C，D四点共圆，则可证得△AHK是等边三角形，然后由AAS即可证得△AKD≌△AHC，则可证得AH+CH=DH．

解：∵四边形ABCD是菱形，

∴AB=BC，

∵AB=AC，

∴AB=BC=AC，

即△ABC是等边三角形，

同理：△ADC是等边三角形

∴∠B=∠EAC=60°，

在△ABF和△CAE中，

，

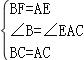∴△ABF≌△CAE（SAS）；

故①正确；

∴∠BAF=∠ACE，

∵∠AEH=∠B+∠BCE，

∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°；

故②正确；

在HD上截取HK=AH，连接AK，

∵∠AHC+∠ADC=120°+60°=180°，

∴点A，H，C，D四点共圆，

∴∠AHD=∠ACD=60°，∠ACH=∠ADH，

∴△AHK是等边三角形，

∴AK=AH，∠AKH=60°，

∴∠AKD=∠AHC=120°，

在△AKD和△AHC中，

，

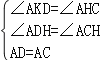∴△AKD≌△AHC（AAS），

∴CH=DK，

∴DH=HK+DK=AH+CH；

故③正确；

故选D．