
 如图,点B、C、D都在半径为12的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为12的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.分析 (1)首先证明四边形ABDC为平行四边形,推出∠A=∠D=30°,∵∠AOC=2∠D=60°,由此可以证明∠ACO=90°即可.
(2)在直角△BEO中,∠OBD=30°,OB=12,推出OE=$\frac{1}{2}$OB=6,BE=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,根据BD=2BE=12$\sqrt{3}$,即可即可解决问题.
(3)易证△OEB≌△CED,推出S阴影=S扇形BOC,由此即可计算.
解答 (1)证明:连接OC,OC交BD于E,
∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∵∠CDB=∠OBD,
∴CD∥AB,
又∵AC∥BD,
∴四边形ABDC为平行四边形,
∴∠A=∠D=30°,
∴∠OCA=180°-∠A-∠COB=90°,即OC⊥AC
又∵OC是⊙O的半径,
∴AC是⊙O的切线;
(2)解:由(1)知,OC⊥AC.
∵AC∥BD,
∴OC⊥BD,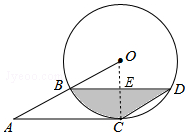
∴BE=DE,
∵在直角△BEO中,∠OBD=30°,OB=12,
∴OE=$\frac{1}{2}$OB=6,BE=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
∴BD=2BE=12$\sqrt{3}$;
(3)解:在△OEB和△CED中,
$\left\{\begin{array}{l}{OE=EC}\\{∠OEB=∠CED}\\{BE=DE}\end{array}\right.$,
∴△OEB≌△CED,
∴S阴影=S扇形BOC
∴S阴影=$\frac{60π•1{2}^{2}}{360}$=24π.
答:阴影部分的面积是24π.
点评 本题考查切线的判定、垂径定理、扇形的面积公式,全等三角形的判定和性质.平行四边形的判定和性质等知识,解题的关键是发现四边形ABDC是平行四边形,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | -6、1 | B. | 6、1 | C. | 6、-1 | D. | -6、-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
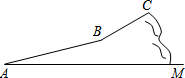 今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔191米,C点海拔791米.
今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔191米,C点海拔791米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com